PQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
203cm
214cm
103cm
154cm
The correct Answer is:A
To find the length of TP in the given problem, we can follow these steps:
Step 1: Understand the Geometry
We have a circle with center O and radius 5 cm. The chord PQ has a length of 8 cm. We need to find the length of the tangent TP where T is the point where the tangents at points P and Q intersect.
Step 2: Find the Midpoint of Chord PQ
Let R be the midpoint of chord PQ. Since PQ=8 cm, we have:
PR=RQ=PQ2=82=4 cm
Step 3: Use the Right Triangle
In triangle PRO, where O is the center of the circle, we can apply the Pythagorean theorem. Since OP is the radius, we have:
OP=5 cm(radius)
PR=4 cm(half of the chord)
We need to find OR:
OR2+PR2=OP2
Substituting the known values:
OR2+42=52
OR2+16=25
OR2=25−16=9
OR=√9=3 cm
Step 4: Apply Similar Triangles
Now, consider triangles TPR and PRO. Since TP is tangent to the circle at point P, angle TPR is 90∘. Thus, triangles TPR and PRO are similar by AA (Angle-Angle) similarity.
Step 5: Set Up the Proportions
From the similarity of triangles:
TPPO=PROR
Substituting the known lengths:
TP5=43
Step 6: Solve for TP
Cross-multiplying gives:
TP⋅3=4⋅5
3TP=20
TP=203 cm
Final Answer
Thus, the length of TP is 203 cm.
---
We have a circle with center O and radius 5 cm. The chord PQ has a length of 8 cm. We need to find the length of the tangent TP where T is the point where the tangents at points P and Q intersect.
Let R be the midpoint of chord PQ. Since PQ=8 cm, we have:
PR=RQ=PQ2=82=4 cm
In triangle PRO, where O is the center of the circle, we can apply the Pythagorean theorem. Since OP is the radius, we have:
OP=5 cm(radius)
PR=4 cm(half of the chord)
We need to find OR:
OR2+PR2=OP2
Substituting the known values:
OR2+42=52
OR2+16=25
OR2=25−16=9
OR=√9=3 cm
Now, consider triangles TPR and PRO. Since TP is tangent to the circle at point P, angle TPR is 90∘. Thus, triangles TPR and PRO are similar by AA (Angle-Angle) similarity.
From the similarity of triangles:
TPPO=PROR
Substituting the known lengths:
TP5=43
Cross-multiplying gives:
TP⋅3=4⋅5
3TP=20
TP=203 cm
Thus, the length of TP is 203 cm.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIV)90videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - TRY YOURSELF25videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XII)90videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself10videos
DISCOUNT
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
Similar Questions
In the adjoining figure, AB is a chord of length 9.6 cm of a circle with centre O and radius 6 cm. The tangents at A and B intersect at P. Find the length of PA.
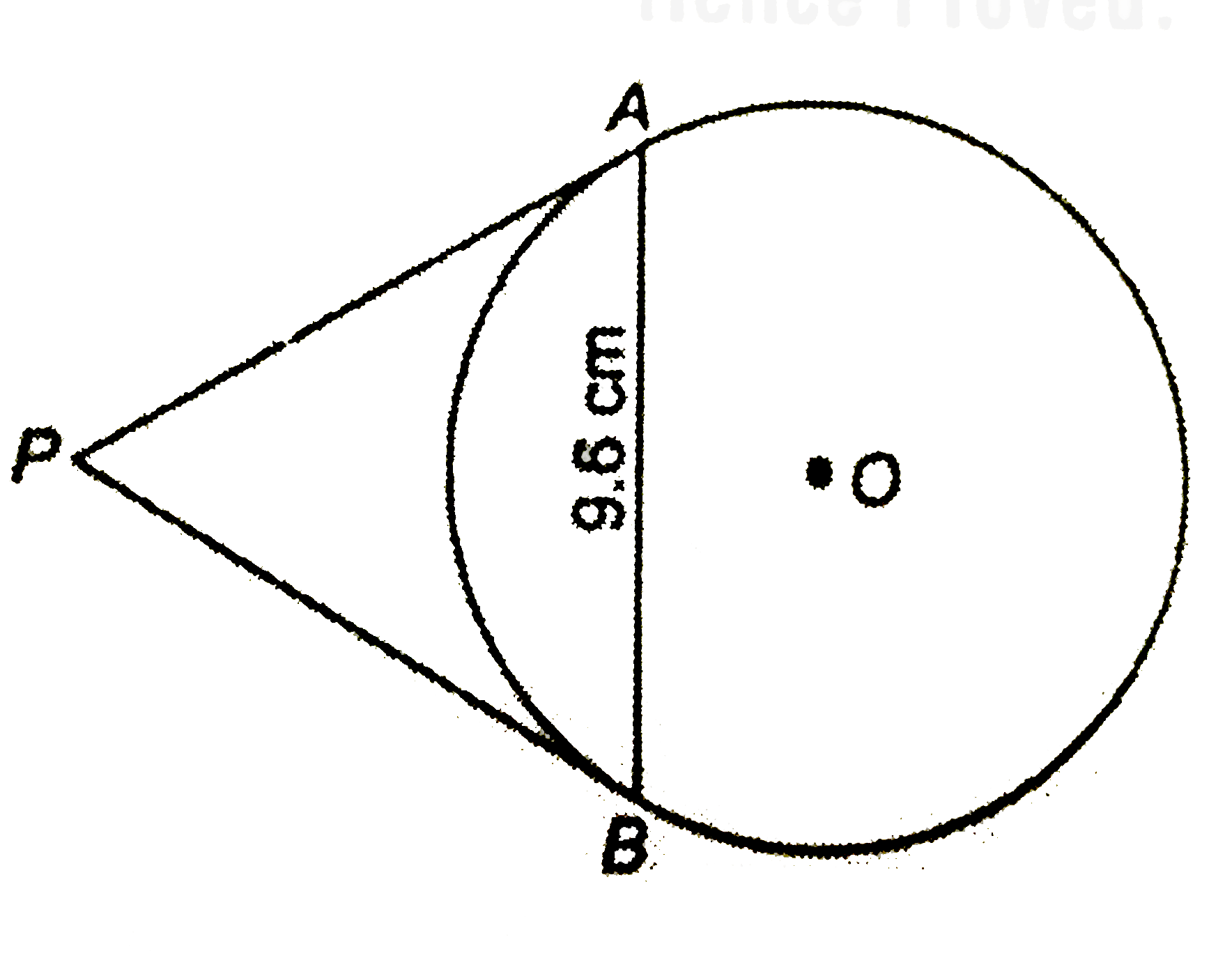 View Solution
View SolutionPQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T . Find the length TP .
View Solution
Knowledge Check
- Question 1 - Select One
PQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
A203cmB214cmC103cmD154cm - Question 2 - Select One
PQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
A163 cmB203 cmC185 cmD196 cm - Question 3 - Select One
PQ is chord of length 6 cm of a circle of radius 5 cm. Tangents to the circle at P and Q meet at T. Length of TP is
A4.75 cmB2.75 cmC3.75 cmD4.25 cm
PQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
View SolutionAB is a chord of length 24cm of a circle of radius 13cm .The tangents at A and B intersect at a point C. Find the length AC
View SolutionIn Fig , PQ is a chord of length 16 cm, of a radius 10 cm . The tangents at P and Q intersect at a point T. Find the length of TP.
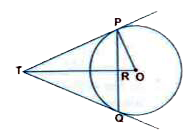 View Solution
View SolutionA chord AB of length 16 cm is drawn in a circle of diameter 20 cm. If tangents at A and B intersect each other at point P, find the length of PA.
View SolutionIn Fig , AB is a chord of a circle , with centre O , such that AB = 16 cm and radius of circle is 10 cm. Tangents at A and B intersect each other at P . Find the length of PA.
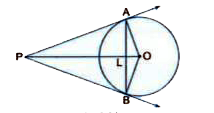 View Solution
View Solution

