Let l1andl2 be the two skew lines. If P, Q are two distinct points on l1 and R, S are two distinct points on l2, then prove that PR cannot be parallel to QS.
To prove that the line segment PR cannot be parallel to the line segment QS, we start with the definitions and properties of skew lines.
1. Define the Skew Lines:
Let the skew lines l1 and l2 be represented as:
l1:→r=→A+λ→B(1)
l2:→r=→C+μ→D(2)
where →A and →C are position vectors of points on lines l1 and l2, respectively, and →B and →D are direction vectors of lines l1 and l2, respectively.
2. Identify Points on the Lines:
Let P and Q be points on line l1:
P:→P=→A+λ1→B(3)
Q:→Q=→A+λ2→B(4)
Let R and S be points on line l2:
R:→R=→C+μ1→D(5)
S:→S=→C+μ2→D(6)
3. Express the Vectors PR and QS:
The vector →PR can be expressed as:
→PR=→R−→P=(→C+μ1→D)−(→A+λ1→B)=→C−→A+μ1→D−λ1→B(7)
The vector →QS can be expressed as:
→QS=→S−→Q=(→C+μ2→D)−(→A+λ2→B)=→C−→A+μ2→D−λ2→B(8)
4. Condition for Parallelism:
For the vectors →PR and →QS to be parallel, there must exist a scalar k such that:
→PR=k⋅→QS(9)
This leads to the equation:
→C−→A+μ1→D−λ1→B=k(→C−→A+μ2→D−λ2→B)(10)
5. Equating Components:
From equation (10), we can separate the components:
- Coefficient of →C−→A:
1−k=0⟹k=1(11)
- Coefficient of →D:
μ1−kμ2=0(12)
- Coefficient of →B:
−λ1+kλ2=0(13)
6. Substituting k=1:
Substitute k=1 into equations (12) and (13):
μ1−μ2=0⟹μ1=μ2(14)
−λ1+λ2=0⟹λ1=λ2(15)
7. Conclusion:
The equations μ1=μ2 and λ1=λ2 imply that points R and S would be the same point if PR were parallel to QS, which contradicts the fact that P,Q are distinct points on l1 and R,S are distinct points on l2. Therefore, PR cannot be parallel to QS.
Let the skew lines l1 and l2 be represented as:
l1:→r=→A+λ→B(1)
l2:→r=→C+μ→D(2)
where →A and →C are position vectors of points on lines l1 and l2, respectively, and →B and →D are direction vectors of lines l1 and l2, respectively.
Let P and Q be points on line l1:
P:→P=→A+λ1→B(3)
Q:→Q=→A+λ2→B(4)
Let R and S be points on line l2:
R:→R=→C+μ1→D(5)
S:→S=→C+μ2→D(6)
The vector →PR can be expressed as:
→PR=→R−→P=(→C+μ1→D)−(→A+λ1→B)=→C−→A+μ1→D−λ1→B(7)
The vector →QS can be expressed as:
→QS=→S−→Q=(→C+μ2→D)−(→A+λ2→B)=→C−→A+μ2→D−λ2→B(8)
For the vectors →PR and →QS to be parallel, there must exist a scalar k such that:
→PR=k⋅→QS(9)
This leads to the equation:
→C−→A+μ1→D−λ1→B=k(→C−→A+μ2→D−λ2→B)(10)
From equation (10), we can separate the components:
- Coefficient of →C−→A:
1−k=0⟹k=1(11)
- Coefficient of →D:
μ1−kμ2=0(12)
- Coefficient of →B:
−λ1+kλ2=0(13)
Substitute k=1 into equations (12) and (13):
μ1−μ2=0⟹μ1=μ2(14)
−λ1+λ2=0⟹λ1=λ2(15)
The equations μ1=μ2 and λ1=λ2 imply that points R and S would be the same point if PR were parallel to QS, which contradicts the fact that P,Q are distinct points on l1 and R,S are distinct points on l2. Therefore, PR cannot be parallel to QS.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - CONCEPT APPLICATION EXERCISE 3.319videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - CONCEPT APPLICATION EXERCISE 3.45videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - CONCEPT APPLICATION EXERCISE 3.112videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions294videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)1videos
TRIGONOMETRIC EQUATIONS
Similar Questions
Let l1andl2 be the two skew lines. If P,Q are two distinct points on l1ndR,S are two distinct points on l2, then prove that PR cannot be parallel to QS.
View SolutionLet l1 and l2 be the two lines which are normal to y2=4x and tangent to x2=−12y respectively (where, l1andl2 are not the x - axis). Then, the product of the slopes of l1andl2 is
View Solution
Knowledge Check
- Question 1 - Select One
Lines l2andl2 intersect each other and 3 parallel lines, l3,l4andl5, at the points shown in the figure below. The ratio of the perimeter of △ABC to the perimeter of △AFG is 1:3 . The ratio of DE to FG is 2:3. What is the ratio of AC to CE?
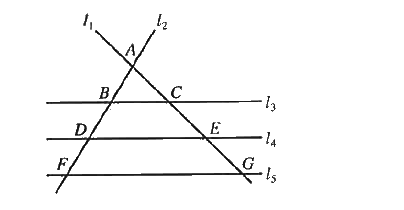 A1:1B1:2C1:3D2:1
A1:1B1:2C1:3D2:1
Let P1andP2 be two planes containing the lines L2andL2 respectively.
STATEMENT-1 : If P1andP2 are parallel then L1andL2 must be parallel.
and
STATEMENT-2 : If P1andP2 are parallel the L1andL2 may not have a common point.View SolutionLet C:y=x2−3,D:y=kx2 be two parabolas and
L1 : x=a,L2:x=1(a≠0) be two straight lines.
IF the line L1 meets the parabola C at a point B on the line L2, other than A, then a may be equal toView SolutionLet L1andL2 be two lines intersecting at P If A1,B1,C1 are points on L1,A2,B2,C2,D2,E2 are points on L2 and if none of these coincides with P, then the number of triangles formed by these 8 points is
View SolutionP is a point equidistant from two lines l and m intersecting at a point A, Show that AP bisects the angle between them.
View SolutionPoints (3, 0) and (-1,0) are invariant points under reflection in the line L1 points (0, -3) and (0, 1) are invariant points on reflection in line L2
Write down the images of P (3,4) and Q (-5,-2) on reflection in L2 Name the images as P" and Q" respectively.View SolutionLet 2a+2b+c=0,l1andl2 are straight lines of the family ax+by+c=0 which are at 1 unit distance from the point (1, 1), then the area (in sq. units) bounded by l1,l2 and coordinate axes is
View SolutionLet L be the set of all straight lines in plane. l1 and l2 are two lines in the set. R1,R2 and R3 are defined relations.
(i) l1R1l2:l1 is parallel to l2
(ii) l1R2l2:l1 is perpendicular to l2
(iii) l1R3l2:l1 intersects l2
Then which of the following is true ?View Solution

