Let M,N, P and Q be the mid points of the edges AB, CD, AC and BD respectively of the tetrahedron ABCD. Further, MN is perpendicular to both AB and CD and PQ is perpendicular to both AC and BD. Then which of the following is/are correct:
AB = CD
BC = DA
AC = BD
AN = BN
The correct Answer is:A, B, C, D
To solve the problem, we need to analyze the tetrahedron ABCD and the midpoints M, N, P, and Q of its edges. We will derive the relationships between the edges based on the given conditions.
1. Identify the Midpoints:
- Let M be the midpoint of edge AB.
- Let N be the midpoint of edge CD.
- Let P be the midpoint of edge AC.
- Let Q be the midpoint of edge BD.
2. Establish the Perpendicular Conditions:
- We are given that line segment MN is perpendicular to both edges AB and CD.
- We are also given that line segment PQ is perpendicular to both edges AC and BD.
3. Analyze the Tetrahedron:
- In a regular tetrahedron, all edges are of equal length. Thus, we can denote the lengths of the edges as follows:
- AB=a
- AC=b
- AD=c
- BC=d
- BD=e
- CD=f
4. Use the Perpendicular Conditions:
- Since MN is perpendicular to both AB and CD, we can conclude that:
- AB is equal to CD (i.e., a=f).
- Similarly, since PQ is perpendicular to both AC and BD, we can conclude that:
- AC is equal to BD (i.e., b=e).
5. Establish Relationships:
- From the perpendicular conditions, we can derive:
- a=f (from MN)
- b=e (from PQ)
- Additionally, since MN and PQ are midpoints, we can conclude:
- BC=AD (i.e., d=c).
6. Summarize the Results:
- From the analysis, we have the following equalities:
- AB=CD
- AC=BD
- BC=AD
- AN=BN (since M and N are midpoints, and angles ∠ABN=∠ABM are equal).
Conclusion:
Thus, the correct relationships are:
- AB=CD
- AC=BD
- BC=AD
- AN=BN
- Let M be the midpoint of edge AB.
- Let N be the midpoint of edge CD.
- Let P be the midpoint of edge AC.
- Let Q be the midpoint of edge BD.
- We are given that line segment MN is perpendicular to both edges AB and CD.
- We are also given that line segment PQ is perpendicular to both edges AC and BD.
- In a regular tetrahedron, all edges are of equal length. Thus, we can denote the lengths of the edges as follows:
- AB=a
- AC=b
- AD=c
- BC=d
- BD=e
- CD=f
- Since MN is perpendicular to both AB and CD, we can conclude that:
- AB is equal to CD (i.e., a=f).
- Similarly, since PQ is perpendicular to both AC and BD, we can conclude that:
- AC is equal to BD (i.e., b=e).
- From the perpendicular conditions, we can derive:
- a=f (from MN)
- b=e (from PQ)
- Additionally, since MN and PQ are midpoints, we can conclude:
- BC=AD (i.e., d=c).
- From the analysis, we have the following equalities:
- AB=CD
- AC=BD
- BC=AD
- AN=BN (since M and N are midpoints, and angles ∠ABN=∠ABM are equal).
Thus, the correct relationships are:
- AB=CD
- AC=BD
- BC=AD
- AN=BN
Topper's Solved these Questions
- VECTOR & 3DIMENSIONAL GEOMETRYBOOK - VK JAISWAL ENGLISHCHAPTER - VECTOR & 3DIMENSIONAL GEOMETRYEXERCISE - Exercise-3 : Comprehension Type Problems
13 Videos
- VECTOR & 3DIMENSIONAL GEOMETRYBOOK - VK JAISWAL ENGLISHCHAPTER - VECTOR & 3DIMENSIONAL GEOMETRYEXERCISE - Exercise-5 : Subjective Type Problems
13 Videos
- VECTOR & 3DIMENSIONAL GEOMETRYBOOK - VK JAISWAL ENGLISHCHAPTER - VECTOR & 3DIMENSIONAL GEOMETRYEXERCISE - Exercise-5 : Subjective Type Problems
13 Videos
- TRIGONOMETRIC EQUATIONS BOOK - VK JAISWAL ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONS EXERCISE - Exercise-5 : Subjective Type Problems
9 Videos
Similar Questions
In ΔABC,AB=AC.D,Eand F are mid-points of the sides BC, CA and AB respectively . Show that :
AD is perpendicular to EF.
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rhombus and P, Q, R and S are wthe mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionM and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. Prove that :
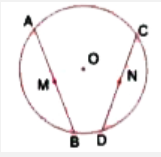
∠AMN=∠CNM.
View SolutionM and N are mid-point of the diagnols AC and BD respectivley of quadrilateral ABCD, then¯¯¯¯¯¯AB+¯¯¯¯¯¯AD+¯¯¯¯¯¯CB+¯¯¯¯¯¯CD=
View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

View SolutionIn the given figure, AC is perpendicular to line PQ and BC = CD. Show that AE is greater than AB.
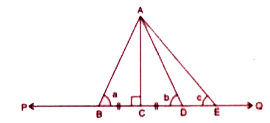
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD.

View SolutionABCD is a square. P, Q and Rare the points on AB, BC and CD respectively, such that AP = BQ = CR. Prove that:
PQ = QR
View SolutionABCD is a regular tetrahedron P & Q are the mid -points of the edges AC and AB respectively, G is the cenroid of the face BCD and θ is the angle between the vectors −−→PG and −−→DQ, then
View Solution
