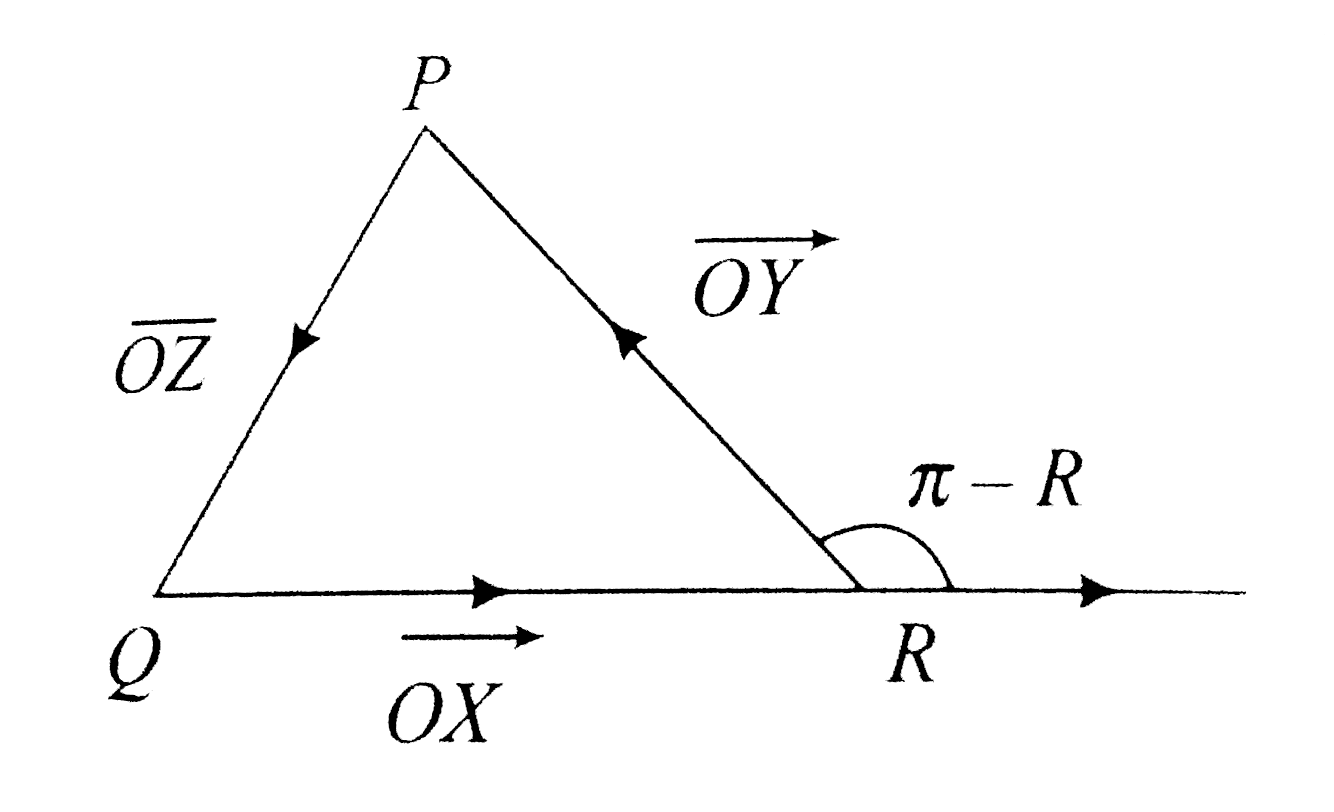
Let O be the origin, and OXxOY,OZ be three unit vectors in the direction of the sides QR , RP , PQ , respectively of a triangle PQR. If the triangle PQR varies, then the minimum value of cos(P+Q)+cos(Q+R)+cos(R+P) is: −32 (b) 53 (c) 32 (d) −53Solution in Bengali
−53
−32
32
53
The correct Answer is:B
−(cosP+cosQ+cosR)
=−−→OX.−−→OY+−−→OZ+−−→OZ.−−→OX
=(−−→OX+−−→OY+−−→OZ)2−(∣∣∣−−→OX∣∣∣2+∣∣∣−−→OY∣∣∣2+∣∣∣−−→OZ∣∣∣2)2≥−32
Topper's Solved these Questions
- JEE 2019BOOK - CENGAGE PUBLICATIONCHAPTER - JEE 2019EXERCISE - chapter -3
1 Videos
- JEE 2019BOOK - CENGAGE PUBLICATIONCHAPTER - JEE 2019EXERCISE - MCQ
92 Videos
- JEE 2019BOOK - CENGAGE PUBLICATIONCHAPTER - JEE 2019EXERCISE - chapter -2
1 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - All Questions
541 Videos
- LIMITSBOOK - CENGAGE PUBLICATIONCHAPTER - LIMITSEXERCISE - Comprehension Type
4 Videos
Similar Questions
The equation of the plane passing through the point (1,1,1) and perpendicular to the planes 2x+y−2z=5and3x−6y−2z=7
View SolutionIn a class 140 students numbered 1 to 140, all even numbered students opted Mathematics course, those whose number is divisible by 3 opted Physics course and those whose number is divisible by 5 opted Chemistry course. Then the number of students who did not opt for any of the three courses is (a) 38 (b) 1 (c)42 (d) 102
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
View SolutionFind x satisfying [tanx]+[cotx]=2, where [.] represents the greatest integer function.
View Solutionlimx→0sin2xx
View SolutionLet O be the origin, and OXxOY,OZ be three unit vectors in the direction of the sides QR , RP , PQ , respectively of a triangle PQR. If the triangle PQR varies, then the minimum value of cos(P+Q)+cos(Q+R)+cos(R+P) is: −32 (b) 53 (c) 32 (d) −53
View SolutionLet O be the origin, and OX,OY,OZ be three unit vectors in the direction of the sides QR , RP , PQ , respectively of a triangle PQR. |OX×OY|= s∈(P+R) (b) sin2R (c)sin(Q+R) (d) sin(P+Q).
View SolutionLet O be the origin and OX, OY, OZ be three unit vectors in the directions of the sides, QP, RP, QR respectively of a △PQR.
Q. If the triangle PQR varies, then the minimum value of cos(P+Q)+cos(Q+R)+cos(R+P) is
View Solutionमानाकि O मूलबिन्दु है एवं त्रिभुज PQR की भुजाओं −−→QR,−−→RP,−−→PQ, की दिशाओं में तीन एकांक सदिश क्रमश: −−→OX,−−→OY,−−→OZ हैं |
यदि त्रिभुज PQR परिवर्ती है तब,
cos(P+Q)+cos(Q+R)+cos(R+P) का न्यूनतम मान है
View Solutionयदि किसी त्रिभुज PQR के कोण P,Q,R,,cosP=sinQ2sinR को संतुष्ट करते हो तो त्रिभुज होगा
View SolutionThe triangle PQR of which the angles P,Q,R satisfy cos P =sinQ2sinR is :
View Solutionযদি PQR একটি পরিবর্তনশীল ত্রিভুজ হয়, তবে cos(P+Q)+cos(Q+R)+cos(R+P) এর সর্বনিম্ন মান হবে–
View SolutionLet O be the origin, and OXxOY,OZ be three unit vectors in the direction of the sides QR , RP , PQ , respectively of a triangle PQR. If the triangle PQR varies, then the minimum value of cos(P+Q)+cos(Q+R)+cos(R+P) is: −32 (b) 53 (c) 32 (d) −53
View Solutionमानाकि O मूलबिन्दु है एवं त्रिभुज PQR की भुजाओं −−→QR,−−→RP,−−→PQ, की दिशाओं में तीन एकांक सदिश क्रमश: −−→OX,−−→OY,−−→OZ हैं |
यदि त्रिभुज PQR परिवर्ती है तब,
cos(P+Q)+cos(Q+R)+cos(R+P) का न्यूनतम मान है
View SolutionLet p,q,r be the sides opposite to the angles P,Q, R respectively in a triangle PQR if 2prsin(P−Q+R2) equals
View SolutionPQR ত্রিভুজে P,Q,R কোণের বিপরীত বাহুগুলি যথাক্রমে p,q,r। তাহলে 2prsin(P−Q+R2) - এর মান হল
View Solution
