Let O(0,0), A(2,0) and B(1,1√3) be the vertices of a triangle Let R be the region consisting of all those point P inside ΔOAB which satisfy d(P,OA)≤ min[d(P,OB),d(P,AB)], where d denotes the distance from the point to the corresponding line.
Sketch the region R and find its area. Solution in Tamil
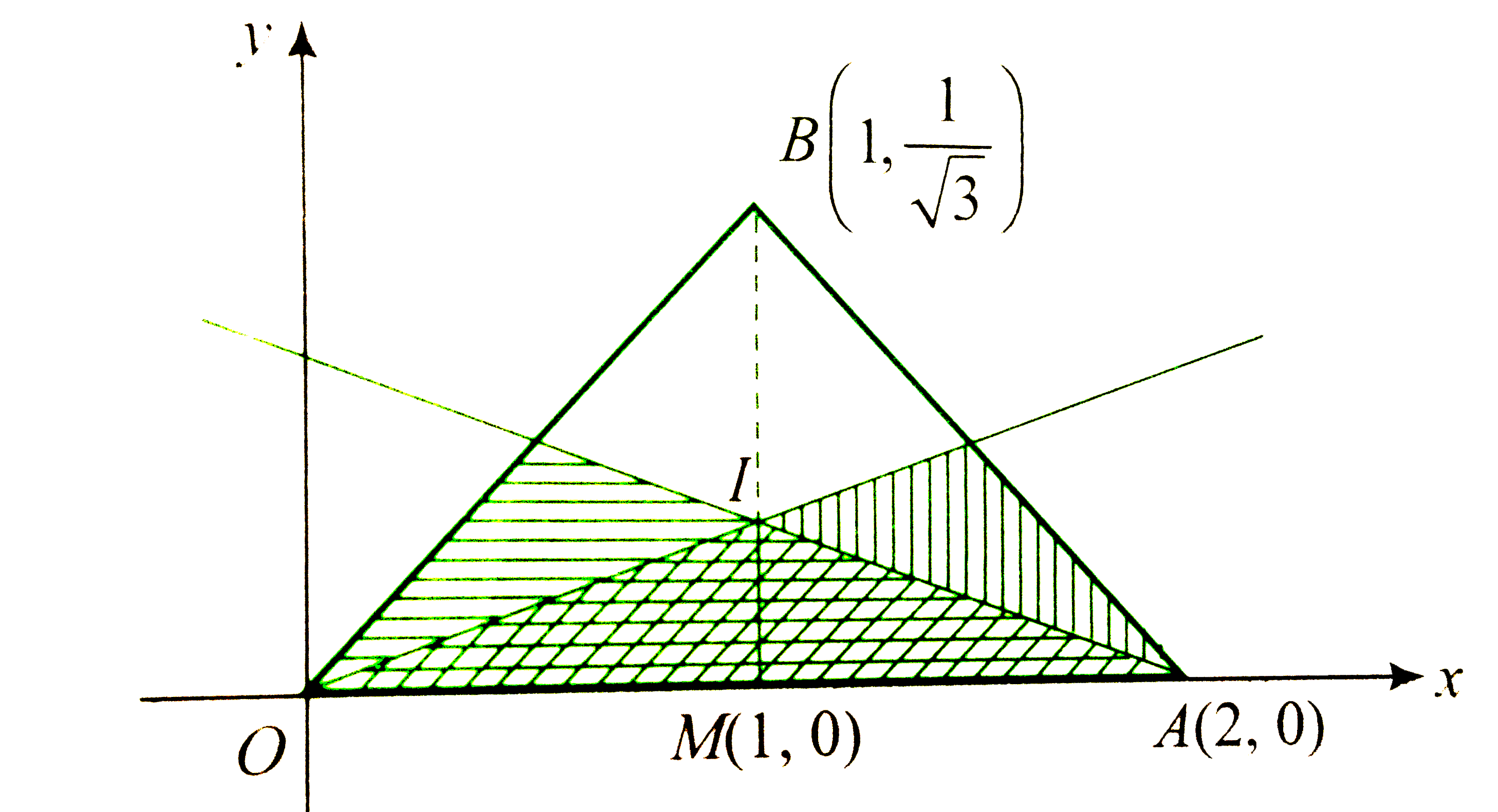
d(P,OA)≤ min [d(P,OB),d(P,AB)]
⇒ d(P,OA)≤d(P,OB)andd(P,OA)≤d(P,AB)
When d(P,OA)=d(P,OB),P is equidistant from OA and OB, or
P lies on the angular bisector of lines OA and OB.
Hence when d(P,OA)≤d(P,OB), point P is nearer to OA than to
OB, i.e., lies on or below the bisector of OA and OB.
Similarly, when d(P,OA)≤d(P,AB), P is nearer to OA then to OB, i.e., lies on or below the bisector of OA and AB.
∴ Required area = Area of ΔOIA.
Now, tan ∠BOA=1/√31=1√3
or ∠BOA=30∘⇒∠IOA=15∘
⇒ IM=tan15∘=2−√3.
Hence, Area of ΔOIA=12OA×IM=12×2×(2−√3)
2−√3 sq. units.
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.1
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.2
14 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
10 Videos
Similar Questions
Find the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
View SolutionFind the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionLet O(0,0),A(2,0),andB(11√3) be the vertices of a triangle. Let R be the region consisting of all those points P inside OAB which satisfy d(P,OA)≤min[d(p,OB),d(P,AB)] , where d denotes the distance from the point to the corresponding line. Sketch the region R and find its area.
View SolutionLet O(0.0),A(6,0) and B(3,sqrt3) be the vertices of triangle OAB. Let R those points P inside triangle OAB which satisfy d(P, OA) minimum (d(P,OB),d(P,AB) where d(P, OA), d(P, OB) and d(P, AB) represent the distance of P from the sides OA, OB and AFB respectively. If the area of region R is 9 (a -sqrtb) where a and b are coprime, then find the value of (a+ b)
View SolutionA(3, 4),B(0,0) and c(3,0) are vertices of DeltaABC. If 'P' is the point inside the DeltaABC, such that d(P, BC)le min. {d(P, AB), d (P, AC)}. Then the maximum of d (P, BC) is.(where d(P, BC) represent distance between P and BC).
View SolutionLet ABC be a triangle with vertices A-=(6,2sqrt(3)+1)) ) B-=(4,2) and C-=(8,2). Let R be the region consisting of all those points P inside Delta ABC which satisfyd (P,BC)>=max{d(P,AB);d(P,AC)}, where d(P,L) denotes the distance of the point from the line L,then
View SolutionLet d(P, OA) le min {d (P, AB), d(P, BC), d (P, OC)} where d denotes the distance from the point to the corresponding line and S be the region consisting of all those points P inside the rectangle OABC such that O = (0, 0), A = (3, 0), B = (3, 2) and C = (0, 2), which satisfy the above relation, then area of the region S is
View SolutionLet O(0,0),A(2,0) be the vertices of an isosceles triangle inscribed in an ellipse (x-1)^(2)+3y^(2)=1. Let s represents the region consisting all those points P inside the given triangle which stales that,Distance of pistance of point p from the other two mides of the triangle
View SolutionConsider the traingle having vertices O(0,0),A(2,0), and B(1,√3). Also b≤min{a1,a2,a3....an} means b≤a1 when a1 is least, b≤a2 when a2 is least, and so on. Form this, we can say b≤a1,b≤a2,.....b≤an.
Let R be the region consisting of all those points P inside ΔOAB which satisfy d(P,OA)≤min[d(P,OB),d(P,AB)], where d denotes the distance from the point to the corresponding line. then the area of the region R is
View SolutionLet O(0, 0) and B(1,1√3) be the vertices of a triangle. Let R be the region consisting of all those points P inside ΔOAB satisfying. d(P,OA)lr min {d(P,OB),d(P,AB)}, where d denotes the distance from the point P to the corresponding line. Let M be peak of region R.
The perimeter of region R is equal to
View SolutionLet O(0,0),A(2,0)andB(1,1√3) be the vertices of a triangle. Let R be the region consisting of all those points P inside ΔOAB satisfying. d(P,OA)lr min {d(P,OB),d(P,AB)}, where d denotes the distance from the point P to the corresponding line. Let M be peak of region R. The perimeter of region R is equal to
View SolutionLet P(x,y) be a point inside the equilateral ΔABC such that d(P, AB) + d(P, AC) + d(P, BC) = K where k is the altitude of the Δ then
Statement - 1 area of the region of p (x,y) or of (ΔABC)
Statement - 2, For equilateral tringle if d (P,AB) + d(P,AC) + d(P,BC) = k then P will lie inside the pedal triangle of ΔABC
View Solutionमाना O(0,0), A(6,0) एवं B(3,√3) त्रिभुज OAB के शीर्ष है तथा R त्रिभुज OAB के अंदर स्थित उन सभी बिन्दुओं P से निर्मित है जो कि संबंध d(P,OA)≤ न्यूनतम मान (d(P,OB),d(P,AB)) को संतुष्ट करते है जहाँ d(P,OA),d(P,OB) तथा d(P,AB) क्रमशः बिन्दु P से भुजाओं OA, OB एवं AB कि दूरियों को दर्शाते है यदि क्षेत्र R का क्षेत्रफल 9(a−√b) है जहाँ a एवं b सहभाज्य है तो (a+b) का मान ज्ञात कीजिये।
View SolutionLet O(0,0),A(2,0),andB(11√3) be the vertices of a triangle. Let R be the region consisting of all those points P inside OAB which satisfy d(P,OA)≤min[d(p,OB),d(P,AB)] , where d denotes the distance from the point to the corresponding line. Sketch the region R and find its area.
View Solution
