Let O(0,0),A(2,0),andB(11√3) be the vertices of a triangle. Let R be the region consisting of all those points P inside OAB which satisfy d(P,OA)≤min[d(p,OB),d(P,AB)] , where d denotes the distance from the point to the corresponding line. Sketch the region R and find its area.
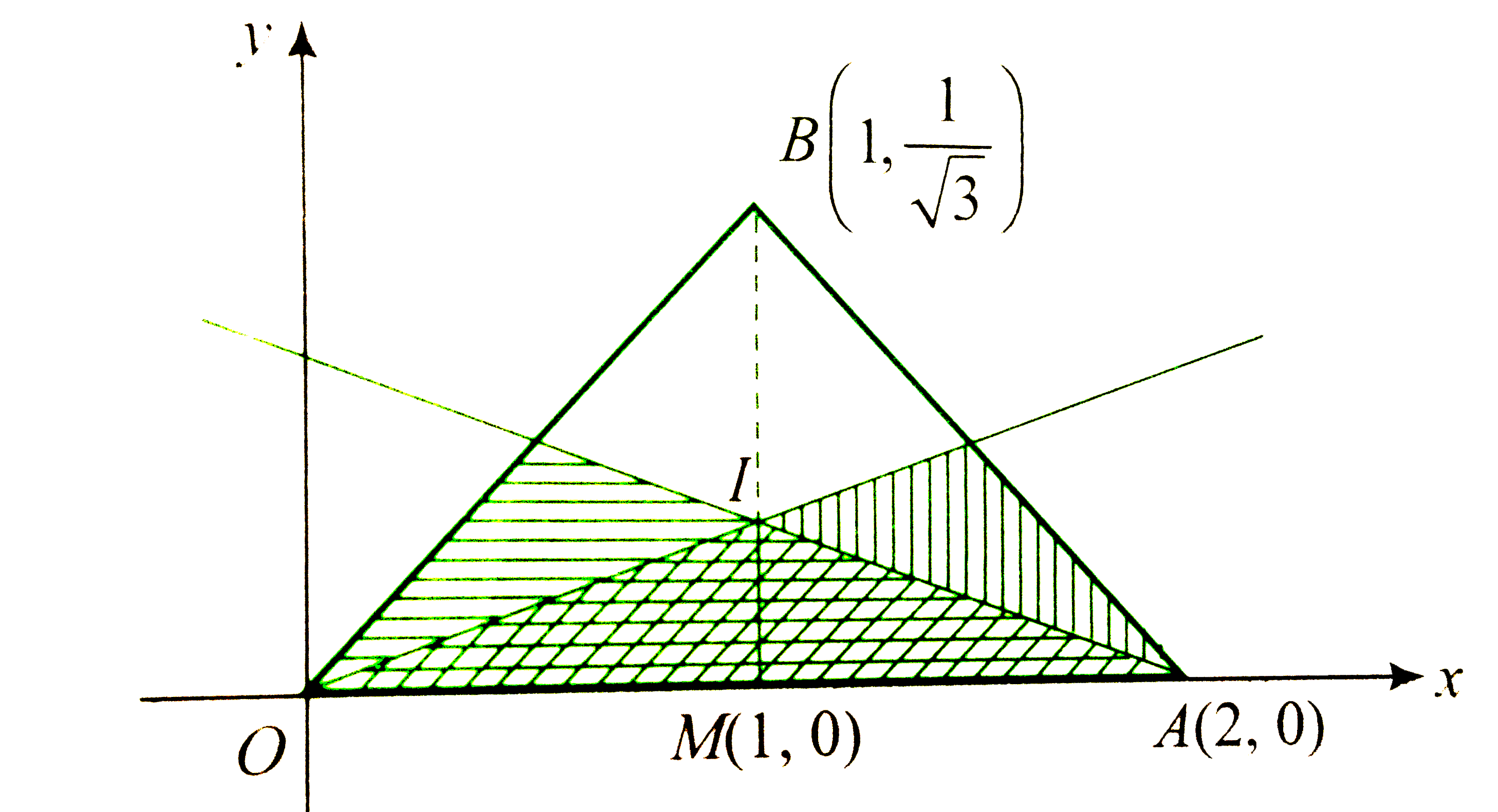
d(P,OA)≤ min [d(P,OB),d(P,AB)]
⇒ d(P,OA)≤d(P,OB)andd(P,OA)≤d(P,AB)
When d(P,OA)=d(P,OB),P is equidistant from OA and OB, or
P lies on the angular bisector of lines OA and OB.
Hence when d(P,OA)≤d(P,OB), point P is nearer to OA than to
OB, i.e., lies on or below the bisector of OA and OB.
Similarly, when d(P,OA)≤d(P,AB), P is nearer to OA then to OB, i.e., lies on or below the bisector of OA and AB.
∴ Required area = Area of ΔOIA.
Now, tan ∠BOA=1/√31=1√3
or ∠BOA=30∘⇒∠IOA=15∘
⇒ IM=tan15∘=2−√3.
Hence, Area of ΔOIA=12OA×IM=12×2×(2−√3)
2−√3 sq. units.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.19videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.214videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank29videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank20videos
AREA UNDER CURVES
Similar Questions
Let ABC be a triangle with vertices A≡(6,,2√3+1))),B≡(4,2)andC≡(8,2). Let R be the region consisting of all those points P inside ΔABC which satisfyd(P,BC)≥max{d(P,AB);d(P,AC)}, where d(P, L) denotes the distance of the point from the line L, then
View SolutionLet O(0.0),A(6,0) and B(3,√3) be the vertices of △OAB. Let R those points P inside △OAB which satisfy d(P, OA) minimum (d(P,OB),d(P,AB) where d(P, OA), d(P, OB) and d(P, AB) represent the distance of P from the sides OA, OB and AFB respectively. If the area of region R is 9(a−√b) where a and b are coprime, then find the value of (a+ b)
View Solution
Knowledge Check
- Question 1 - Select One
Let O(0, 0) and B(1,1√3) be the vertices of a triangle. Let R be the region consisting of all those points P inside ΔOAB satisfying. d(P,OA)lr min {d(P,OB),d(P,AB)}, where d denotes the distance from the point P to the corresponding line. Let M be peak of region R.
The perimeter of region R is equal toA√3B1√3C3D2−√3 - Question 2 - Select One
Let O(0,0),A(2,0)andB(1,1√3) be the vertices of a triangle. Let R be the region consisting of all those points P inside ΔOAB satisfying. d(P,OA)lr min {d(P,OB),d(P,AB)}, where d denotes the distance from the point P to the corresponding line. Let M be peak of region R. The perimeter of region R is equal to
A4−√3B4+√3C4+3√3D2+4√(2−√3) - Question 3 - Select One
Consider the traingle having vertices O(0,0),A(2,0), and B(1,√3). Also b≤min{a1,a2,a3....an} means b≤a1 when a1 is least, b≤a2 when a2 is least, and so on. Form this, we can say b≤a1,b≤a2,.....b≤an.
Let R be the region consisting of all those points P inside ΔOAB which satisfy d(P,OA)≤min[d(P,OB),d(P,AB)], where d denotes the distance from the point to the corresponding line. then the area of the region R isA√3sq,unitsB(2+√3) sq.unitsC√3/2 sq.unitsD1/√3 sq.units
Let O(0,0),A(2,0) be the vertices of an isosceles triangle inscribed in an ellipse (x−1)2+3y2=1. Let S represents the region consisting all those points P inside the given triangle which stales that, Distance of point P from OA is not more than the minimum distance of point p from the other two sides of the triangle".
View SolutionLet d(P,OA)≤min{d(P,AB),d(P,BC),d(P,OC)} where d denotes the distance from the point to the corresponding line and S be the region consisting of all those points P inside the rectangle OABC such that O=(0,0),A=(3,0),B=(3,2)andC=(0,2), which satisfy the above relation, then area of the region S is
View SolutionLet O(0, 0), P(3, 4), Q(6, 0) be the vertices of the triangle OPQ. The point R inside the triangle OPQ is such that the triangles OPR, PQR are of equal area. The coordinates of R are
View SolutionLet O(0,0),A(2,0),B(1,1√3) distance of P from the side OA is less than its distance from the syme vertices of a triangle. A point P moves inside the triangle such that the distance of P from the side OA is less than its distance from the sides OB and AB. The area traced by Pis
View SolutionTwo points O(0,0) and A(3,√3) with another point P form an equilateral triangle. Find the coordinates of P.
View Solution

