Let OA, OB, OC be the co-terminal edges of a rectangular parallelopiped of volume V and let p be the vertex opposite to O. Then, [−−→AP−−→BP−−→CP] is equal to
2V
12V
3√3V
0
The correct Answer is:A
Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram whose diagonals meet at P. If O is a fixed point, then −−→OA+−−→OB+−−→OC+−−→OD equals :
View SolutionLet O, O' and G be the circumcentre, orthocentre and centroid of a ΔABC and S be any point in the plane of the triangle.
Statement -1: −−−→O'A+−−−→O'B+−−−→O'C=2−−−→O'O
Statement -2: −→SA+−−→SB+−−→SC=3−−→SG
View Solution
Knowledge Check
Let ABCD be a parallelogram whose diagonals intersect at P and let O be the origin. What is −−→OA+−−→OB+−−→OC+−−→OD equal to
A2−−→OPB4−−→OPC6−−→OPD8−−→OPThe resultant of the three vectors −−→OA,−−→OB and −−→OC shown in figure is
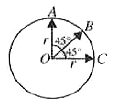 ArB2rCr(1+√s)Dr(√2−1)
ArB2rCr(1+√s)Dr(√2−1)If OACB is a parallelogrma with −−→OC=→a and −−→AB=→b then −−→OA is equal to
A→a+→bB→a−→bC12→a−→bD12→a−→b
Prove that 3−−→OD+−−→DA+−−→DB+−−→DC is equal to −−→OA+−−→OB+−−→OC.
View SolutionOABC is a tetrahedron D and E are the mid points of the edges −−→OA and −−→BC. Then the vector −−→DE in terms of −−→OA,−−→OBand−−→OC
View SolutionIf V is the volume of parallelopiped formed by the vectors →a,→b,→c as three co-terminous edges is 27 cubic units, then the volume of the parallelopiped having →α=→a+2→b−→c,→β=→a−→b and →γ=→a−→b−→c as three coterminous edges is
View SolutionLet O, O' and G be the circumcentre, orthocentre and centroid of a ΔABC and S be any point in the plane of the triangle.
Statement -1: −−−→O'A+−−−→O'B+−−−→O'C=2−−−→O'O
Statement -2: −→SA+−−→SB+−−→SC=3−−→SG
View SolutionStatement 1: Let V1 be the volume of a parallelopiped ABCDEF having →a,→b,→c as three coterminous edges and V2 be the volume of the parallelopiped PQRSTU having three coterminous edges as vectors whose magnitudes are equal to the areas of three adjacent faces of the parallelopiped ABCDEF. Then V2=2V21
Statement 2: For any three vectors →α,→β,→γ
[→α×→β,→β×→γ,→γ×→α]=[→α→β→γ]2
View Solution
