Question

Let $P$
be any moving point on the circle $x^2+y^2-2x=1.AB$
be the chord of contact of this point w.r.t. the circle $x^2+y^2-2x=0$
. The locus of the circumcenter of triangle $CAB(C$
being the center of the circle)
is
$2x^2+2y^2-4x+1=0$

$x^2+y^2-4x+2=0$

$x^2+y^2-4x+1=0$

$2x^2+2y^2-4x+3=0$

Explanation

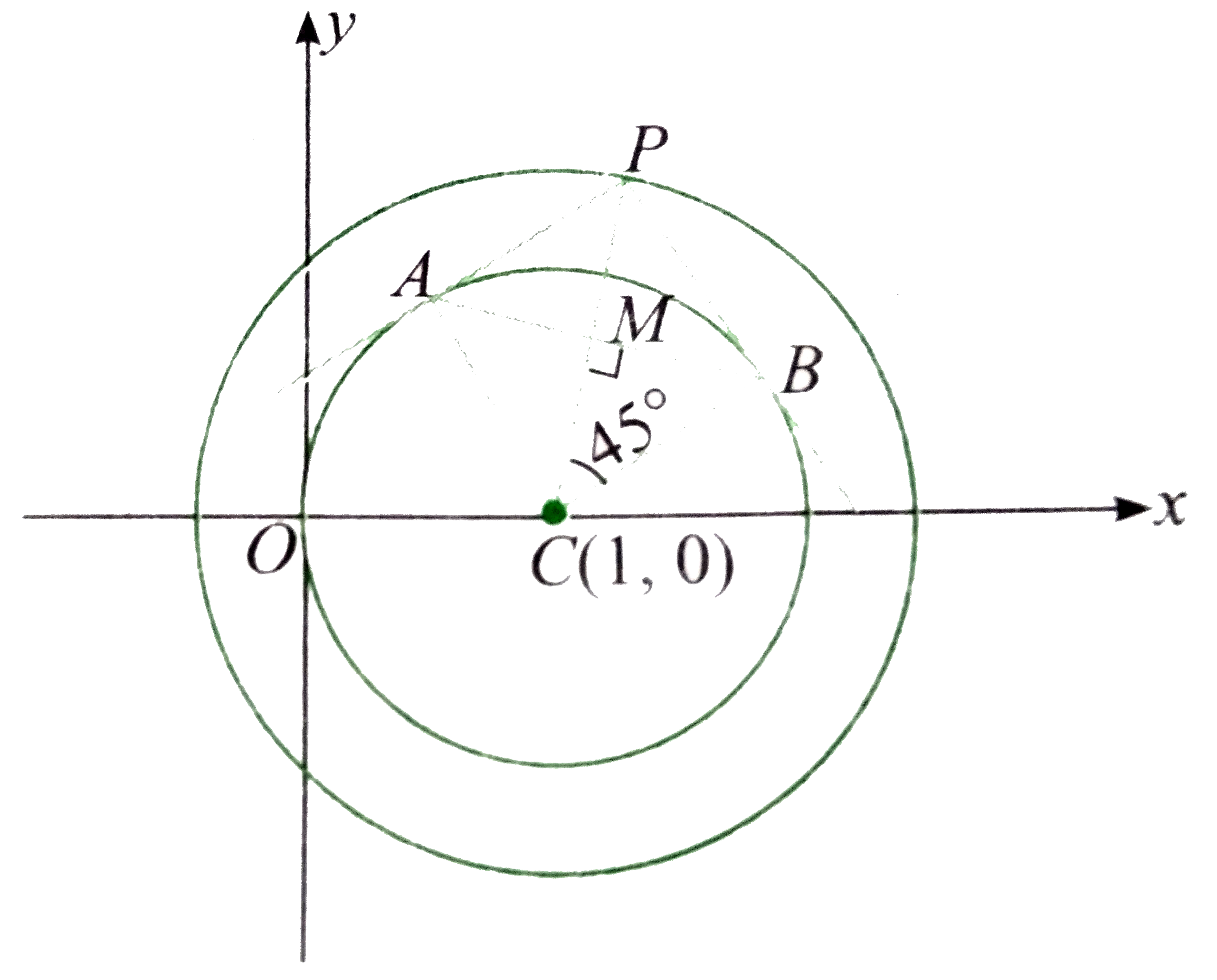
The two circles are
`(x-1)^(2)+y^(2)=1` (1)
`(x-1)^(2)+y^(2)=2` (2)
Clearly, the second circle is the director circle of the first circle.
`:. /_ AB =90^(@)`
S, APBC is square.
Now, circumcentre of the right-angled triangle CAB will be midpoint of hypotenuse.
Let midpoint of AB be M(h,k).
Now, `CM=CB sin 45^(@) =(1)/(sqrt(2))`
So, `(h-1)^(2)+k^(2)=(1)/(2)`
Hence, locus of M is `(x-1)^(2)+y^(2)=(1)/(2)`