Let P be the point (−3,0) and Q be a moving point (0,3t). Let PQ be trisected at R so that R is nearer to Q. RN is drawn perpendicular to PQ meeting the x-axis at N. The locus of the mid-point of RN is Solution in Bengali
(x+3)2−3y=0
(y+3)2−3x=0
x2−y=1
y2−x=1
The correct Answer is:D
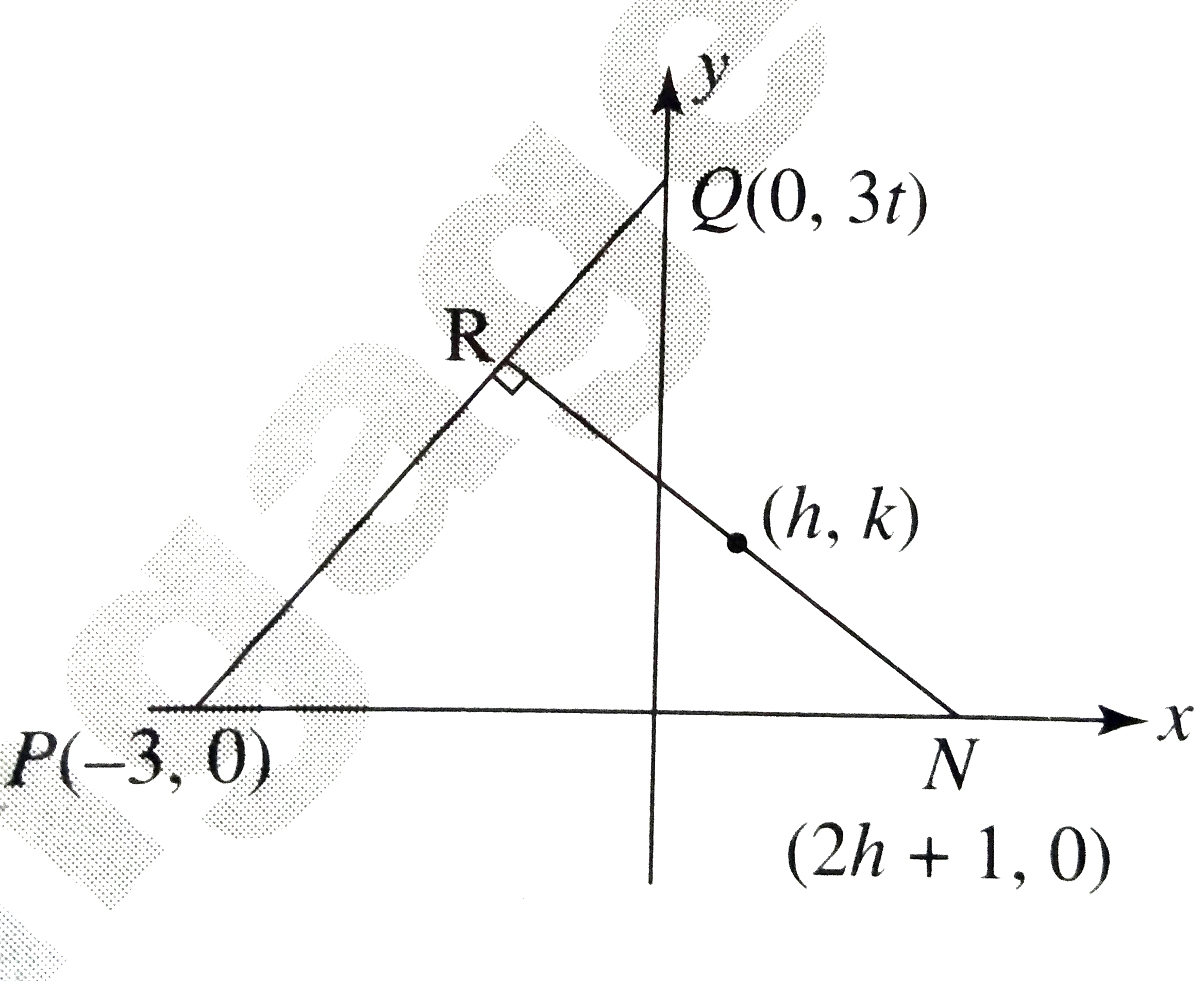
P(−3,0),Q(0,3t),R(−1,2t)
Let the mid point of RN be (h,k)
∴k=t.
RN⊥PQ⇒2t−2h−2×3t3=−1
⇒2t2=2h+2
⇒t2=h+1
⇒k2=h+1
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Comprehension Type4videos
COORDINATE SYSTEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - All Questions238videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - JEE Main6videos
COORDINATE SYSYEM
Similar Questions
A(x1,y1),B(x2,y2),C(x3,y3) are three vertices of a triangle ABC, lx+my+n=0 is an equation of line L. If L intersects the sides BC,CA and AB of a triangle ABC at P,Q,R respectively, then BPPC×CQQA×ARRB is equal to
01:34View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
09:03View SolutionFind x where f(x)=max{√x(2−x),2−x} is non-differentiable.
06:15View SolutionThe lines p(p2+1)x−y+q=0 and (p2+1)2x+(p2+1)y+2q=0 are perpendicular to a common line for
11:30View SolutionThe tangent at any point P on y^(2)=4x meets x-axis at Q, then locus of mid point of PQ will be
05:22View SolutionLet P be the point (−3,0) and Q be a moving point (0,3t). Let PQ be trisected at R so that R is nearer to Q. RN is drawn perpendicular to PQ meeting the x-axis at N. The locus of the mid-point of RN is
03:11View SolutionFrom any point P on the line x = 2y perpendicular is drawn on y = x. Let foot of perpendicular is Q. Find the locus of mid point of PQ.
08:06View SolutionThe tangent to the curve y=x−x3 at a point P meets the curve again at Q. Prove that one point of trisection of PQ lies on the Y-axis. Find the locus of the other points of trisection.
02:05View SolutionIf the coordinates of thepoints P , Q , R are respectively (−7,5),(3,8),(−5,13) and if RN is perpendicular to PQ and RT is parallel to PQ , find the equations of RN and RT.
06:30View SolutionLet P be the point (1,0) and Q a point on the parabola y2=8x, then the locus of mid-point of ¯¯¯¯¯¯PQ is-
04:33View SolutionLet P be (5,3) and a point R on y = x and Q on the X - axis be such that PQ+QR+RP is minimum ,then the coordinates of Q are
02:45View SolutionLet p be the point (1,0) and Q a point on the locurs y^(2)=8x the locus of mid point of PQ is
05:09View SolutionP, Q, R বিন্দু তিনটির স্থানাঙ্ক যথাক্রমে (-7,5), (3,8) (-5,13) হলে এবং RN রেখা PQ এর ওপর লম্ব এবং RT রেখা PQ এর সমান্তরাল হলে RN এবং RT এর সমীকরণ নির্ণয় করো।
02:32View SolutionLet P be (5,3) and a point R on y = x and Q on the X - axis be such that PQ+QR+RP is minimum ,then the coordinates of Q are
02:37View SolutionLet P be the point (−3,0) and Q be a moving point (0,3t). Let PQ be trisected at R so that R is nearer to Q. RN is drawn perpendicular to PQ meeting the x-axis at N. The locus of the mid-point of RN is
02:33View SolutionFrom any point P on the line x = 2y perpendicular is drawn on y = x. Let foot of perpendicular is Q. Find the locus of mid point of PQ.
05:27View Solution

