Let $P M$ be the perpendicular from the point $P (1, 2, 3)$ to the $x - y$ plane. If $- - \to O P$ makes an angle $θ$ with the positive direction of the $z -$ axis and $- - \to O M$ makes an angle $φ$ with the positive direction of $x -$ axis, where $O$ is the origin and $θ$ and $φ$ are acute angels, then If $f (x + y) = f (x) + f (y) - x y - 1$ , $\forall x,$ y in R $and$ f(1)=1, $t h e n t h e ν m b e r o f s o l u t i o n o f$ f(n)=n $,$ n in N , is

A

$cos θ cos ϕ = \frac{1}{\sqrt{14}}$ , $tan ϕ = 2$ , $tan θ = \frac{\sqrt{5}}{3}$

B

$sin θ sin ϕ = \frac{2}{\sqrt{14}}$ , $tan ϕ = 2$ , $tan θ = \frac{\sqrt{5}}{3}$

C

$tan ϕ = 2$ , $cos θ cos ϕ = \frac{1}{\sqrt{14}}$ , $tan θ = \frac{\sqrt{5}}{3}$

D

$tan θ = \frac{\sqrt{5}}{3}$ , $cos θ cos ϕ = \frac{1}{\sqrt{14}}$ , $tan ϕ = 2$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

If $P$ be $(x, y, z),$ then from the figure,
$x = r sin θ cos ϕ, y = r sin θ sin ϕ and z = r cos θ$
$1 = r sin θ cos ϕ, 2 = r sin θ sin ϕ and 3 = r cos θ$

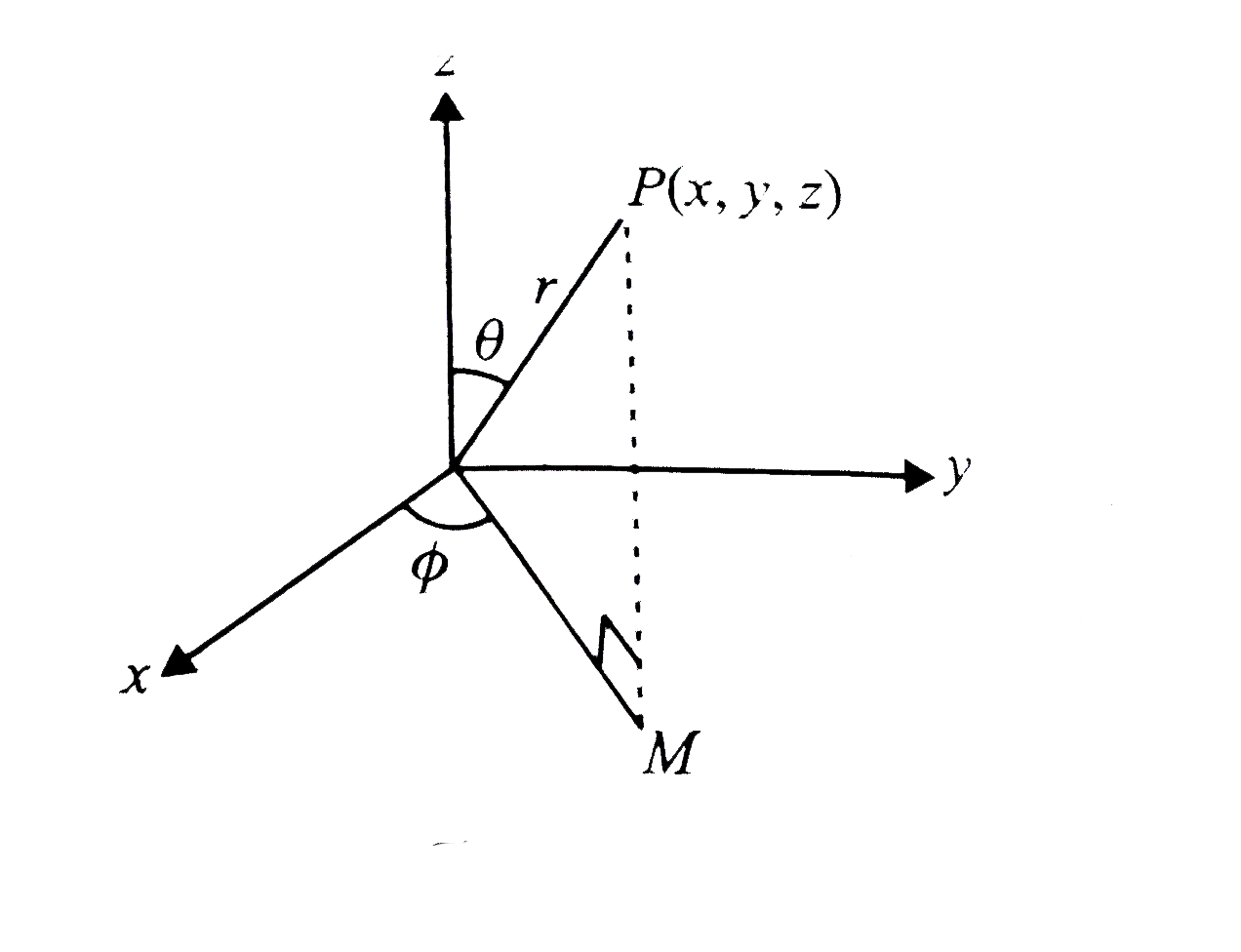
$\Rightarrow 1^{2} + 2^{2} + 3^{2} = r^{2} or r = \pm \sqrt{14}$
$∴ sin θ cos ϕ = \frac{1}{\sqrt{14}}, sin θ sin ϕ$
$= \frac{2}{\sqrt{14}} and cos θ = \frac{3}{\sqrt{14}}$
(neglecting negative sign as $θ and ϕ$ are acute)
$\frac{sin θ sin ϕ}{sin θ cos ϕ} = \frac{2}{1} or tan ϕ = 2$
Also, $tan θ = \sqrt{5} / 3$ .

|

Updated on:21/07/2023

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let PM be the perpendicular from the point $P (1, 2, 3)$ to XY-plane. If OP makes an angle $θ$ with the positive direction of the Z-axies and OM makes an angle $Φ$ with the positive direction of X-axis, where O is the origin, $θ and Φ$ are acute angles, then
A $tan (θ) = \frac{\sqrt{5}}{3}$
B $sin (θ) sin (ϕ) = \frac{2}{\sqrt{14}}$
C $tan (θ) = 2$
D $cos (θ) cos (ϕ) = \frac{1}{\sqrt{14}}$
Question 2 - Select One or More
Let PN be the perpendicular from the point
$P (1, 2, 3)$ to xy-plane. If OP makes an angle $α$
with positive direction of the z-axis and ON makes
an angle $β$ with the positive direction of x-axis,
where O is the origin ( $α and β$ are acute angles),
then
A $sin α sin β = \frac{2}{\sqrt{14}}$
B $cos α cos β = \frac{2}{\sqrt{14}}$
C $tan α = \frac{\sqrt{5}}{3}$
D $tan β = 2$
Question 3 - Select One
If $f (x)$ is a real valued functions satisfying $f (x + y) = f (x) + f (y) - y x - 1$ for all $x, y \in R$ such that $f (1) = 1$ then the number of solutions of $f (n) = n, n \in N$ , is
A1
B2
C3
D4

CENGAGE-THREE-DIMENSIONAL GEOMETRY -Exercise (Multiple)

Home
Ask Doubt
Profile