Question

Let $PM$
be the perpendicular from the point $P(1,2,3)$
to the $x-y$
plane. If $\overrightarrow{O}P$
makes an angle $\theta$
with the positive direction of the $z-$
axis and$\overrightarrow{O}M$
makes an angle $\phi$
with the positive direction of $x-$
axis, $whereO$
is the origin and $\theta and\phi$
are acute angels, then
a. $\cos \theta \cos \phi =1/\sqrt{14}$
b. $\sin \theta \sin \phi =2/\sqrt{14}$

c. $\tan \phi =2$
d. $\tan \theta =\sqrt{5}/3$

Options

A. `costhetacosphi=1//sqrt14`
B. `sinthetasinphi=2//sqrt14`
C. `tanphi=2`
D. `tantheta=sqrt5//3`

Answer

b, c, d

Explanation

If `P` be `(x, y, z),` then from the figure,
`x=r sin theta cosphi, y = rsintheta sin phi and z= rcostheta`
`1=rsintheta cosphi, 2= r sintheta sinphi and 3 = rcostheta`

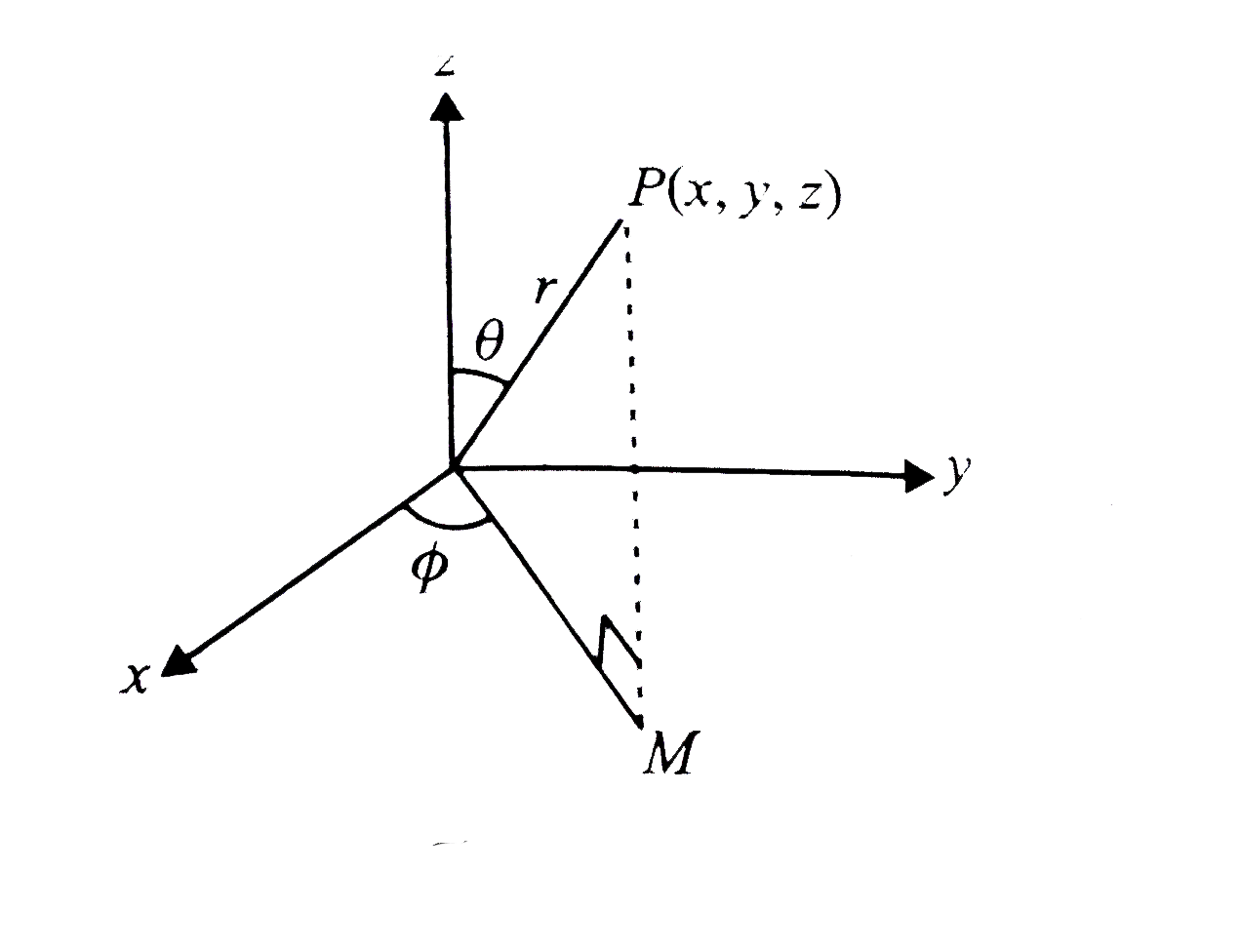
`rArr" "1^(2)+ 2^(2)+3^(2)= r^(2) or r= pm sqrt(14)`
`therefore" "sinthetacosphi = (1)/(sqrt(14)), sin theta sin phi`
`" "=(2)/(sqrt(14)) and cos theta = (3)/(sqrt(14)) `
(neglecting negative sign as `theta and phi` are acute)
`" "(sinthetasinphi)/(sinthetacosphi)=(2)/(1) or tanphi =2`
Also, `tan theta= sqrt(5)//3`.