Let RS be the diameter of the circle x2+y2=1, where S is the point (1,0) Let P be a variable apoint (other than RandS) on the circle and tangents to the circle at SandP meet at the point Q.The normal to the circle at P intersects a line drawn through Q parallel to RS at point E. then the locus of E passes through the point(s)- (A) (13,1√3) (B) (14,12) (C) (13,−1√3) (D) (14,−12)
(13,1√3)
(14,12)
(13,−1√3)
(14,−12)
The correct Answer is:1,3
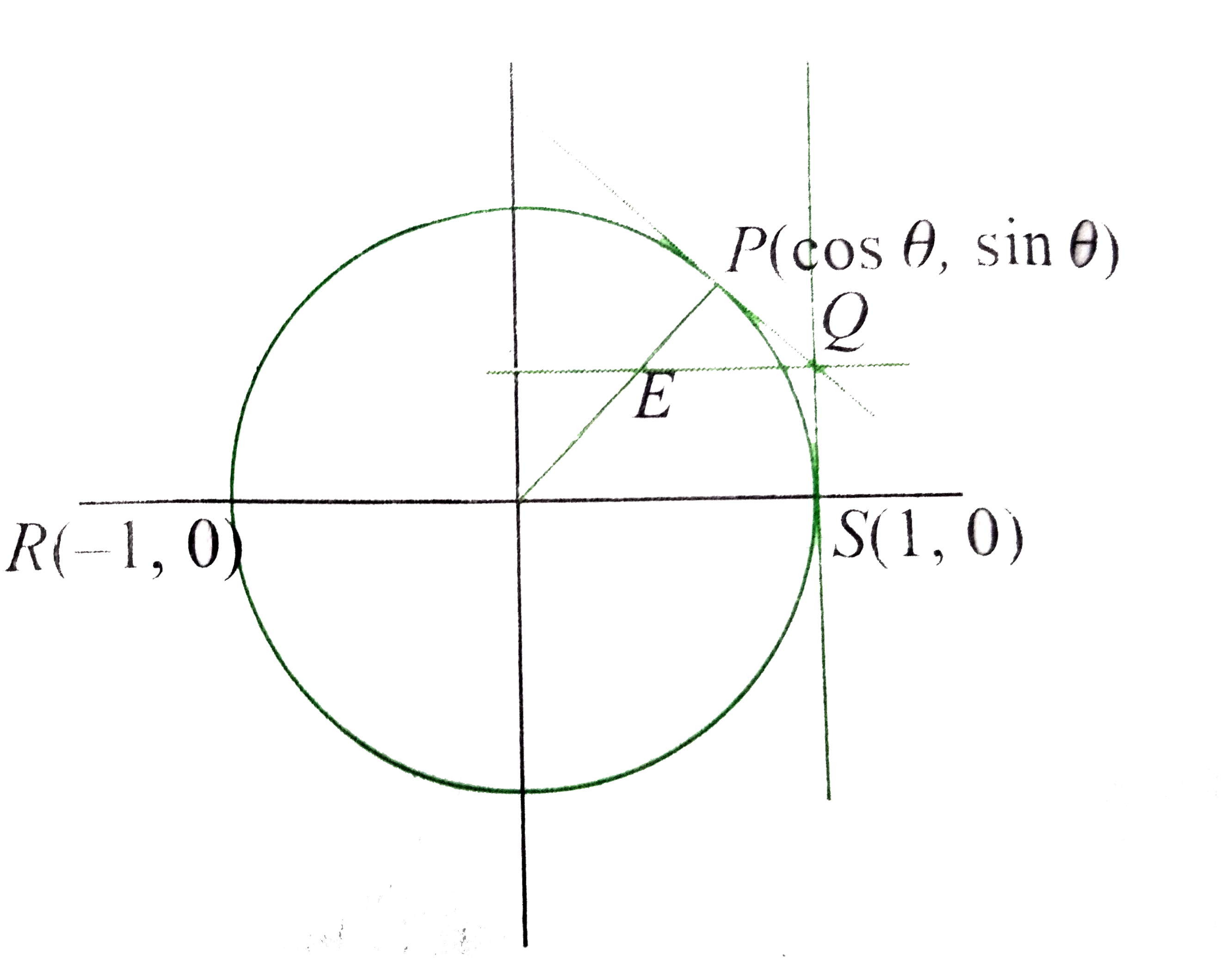
Let point P be (cosθ,sinθ).
Tangent at P is xcosθ+ysinθ=1
∴Q≡(1,1cosθsinθ)
Normal at P,y=tanθx (i)
Equation of QE,y=1−cosθsinθ (ii)
Point E is point of intersection of lines (i) and (ii) .
Eliminating θ from (i) and (ii), we get locus of point E.
From (i) , tanθ=yx
From eq. (ii), we get
y=1−x√x2+y2y√x2+y2=√x2+y2−xy ltbr> or y2+x=√x2+y2
Clearly option (1) and (3) satisfy the above equation.
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - For Problems
43 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Excercises (Single Correct Answer Type)
109 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
A tangent to the circle x2+y2=1 through the point (0, 5) cuts the circle x2+y2=4 at P and Q. If the tangents to the circle x2+y2=4 at P and Q meet at R, then the coordinates of R are
View SolutionIf the tangent to the ellipse x2+2y2=1 at point P(1√2,12) meets the auxiliary circle at point RandQ , then find the points of intersection of tangents to the circle at QandR.
View Solution
Knowledge Check
A tangent to the circle x2+y2=1 through the point (0, 5) cuts the circle x2+y2=4 at P and Q. If the tangents to the circle x2+y2=4 at P and Q meet at R, then the coordinates of R are
A(8√6/5,4/5)B(8√6/5),−4/5)C(−8√6/5),−4/5)Dnone of theseP and Q are two points on circle with centre O. The point R is on the minor arcPQ. The tangents from P and Q meet at S. If ∠PSQ=20∘ them ∠PRQ is-
A80∘B200∘C160∘D100∘
If the tangent to the ellipse x2+2y2=1 at point P(1√2,12) meets the auxiliary circle at point RandQ , then find the points of intersection of tangents to the circle at QandR.
View SolutionThe tangent at any point to the circle x2+y2=r2 meets the coordinate axes at A and B.If the lines drawn parallel to axes through A and B meet at P then locus of P is
View SolutionThe tangent at any point to the circle x2+y2=r2 meets the coordinate axes at A and B. If the lines drawn parallel to axes through A and B meet at P then locus of P is
View SolutionIf the line y=2-x is tangent to the circle S at the point P(1,1) and circle S is orthogonal to the circle x2+y2+2x+2y−2=0 then find the length of tangent drawn from the point (2,2) to the circle S
View SolutionTwo circles intersect at two points P and S. QR is a tangent to the two circles at Q and R. If ∠QSR=72∘, then ∠QPR=.
View Solutionif P is a variable point and PQ and PRare the tangent drawn to the circle x2+y2=9. Let QR be always touching the circle x+y2=4, then locus of P is
View Solution
