The tangent at any point to the circle $x^{2} + y^{2} = r^{2}$ meets the coordinate axes at A and B.If the lines drawn parallel to axes through A and B meet at P then locus of P is

$(\frac{1}{3}, \frac{1}{\sqrt{3}})$

$(\frac{1}{4}, \frac{1}{2})$

$(\frac{1}{3}, - \frac{1}{\sqrt{3}})$

$(\frac{1}{4}, - \frac{1}{2})$

Video Solution

Text Solution

Verified by Experts

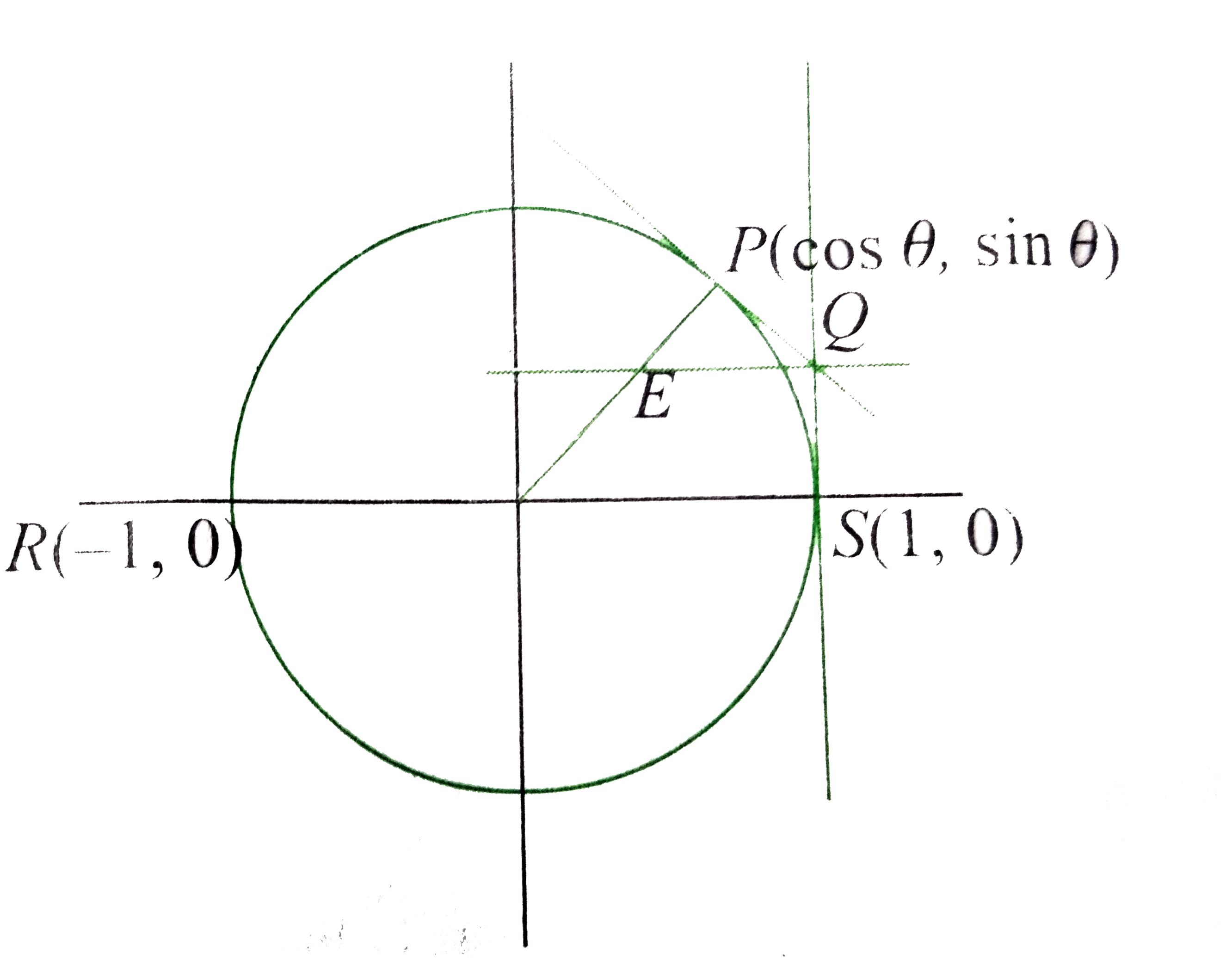
Let point P be $(cos θ, sin θ)$ .
Tangent at P is $x cos θ + y sin θ = 1$
$∴ Q \equiv (1, \frac{1 cos θ}{sin θ})$
Normal at $P, y = tan θ x$ (i)
Equation of QE $, y = \frac{1 - cos θ}{sin θ}$ (ii)
Point E is point of intersection of lines (i) and (ii) .
Eliminating $θ$ from (i) and (ii), we get locus of point E.
From (i) , $tan θ = \frac{y}{x}$
From eq. (ii), we get
y= $\frac{1 - \frac{x}{\sqrt{x^{2} + y^{2}}}}{\frac{y}{\sqrt{x^{2} + y^{2}}}} = \frac{\sqrt{x^{2} + y^{2}} - x}{y}$ ltbr> or $y^{2} + x = \sqrt{x^{2} + y^{2}}$
Clearly option (1) and (3) satisfy the above equation.

The tangent at a point P of a curve meets the y-axis at A, and the line parallel to y-axis at A, and the line parallel to y-axis through P meets the x-axis at B. If area of $Δ O A B$ is constant (O being the origin), Then the curve is
A $c x^{2} - x y + k = 0$
By^(2)+2x^(2)=cx
C $3 x^{2} + 4 y^{2} = k$
D $x y - x^{2} y^{2} + k x = 0$
Any tangent at a point $P (x, y)$ to the ellipse $\frac{x^{2}}{8} + (y^{2}) = 1$ meets the coordinate axes in the points A and B such that the area of the triangle OAB is least, then the point P is
A $(\sqrt{8}, 0)$
B $(0, \sqrt{18})$
C $(2, 3)$
Dnone
A variable line through (p,q) cuts the axes of co ordinates at A and B respectively. Lines are drawn through A parallel to y-axis and through B parallel to x-axis. If they meet at P, then locus of p is
A $\frac{x}{p} + \frac{y}{q} = 1$
B $\frac{p}{x} + \frac{q}{y} = 1$
C $\frac{x}{q} + \frac{y}{p} = 1$
D $\frac{q}{x} + \frac{p}{y} = 1$