Let S be the circle in the xy -plane defined by the equation x2+y2=4. (For Ques. No 15 and 16) Let P be a point on the circle S with both coordinates being positive. Let the tangent to S at P intersect the coordinate axes at the points M and N . Then, the mid-point of the line segment MN must lie on the curve (x+y)2=3xy (b) x2/3+y2/3=24/3 (c) x2+y2=2xy (d) x2+y2=x2y2
(x+y)2=3xy
x2/3+y2/3=24/3
x2+y2=2xy
x2+y2=x2y2
The correct Answer is:4
Let the coordinates of P be (2cosθ,2sinθ)
Equation of tangent to circle at P is xcosx+ysinθ=2
∴M(2cosθ,0),N(0,2cosθ)
Let the mid -point of MN be (x,y)
∴x=1cosθ and y=1sinθ
Squaring and adding , we get
1x2+1y2=1
or x2+y2=x2y2, this is the required locus
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE
7 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - LINKED COMPREHENSION TYPE (For problem 1 and 2)
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
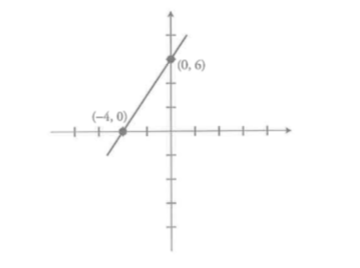
What is the intersection point of the lines defined by the equations 2x+y=7and3x−2y=21?
View SolutionLet P be any point on the curve x2/3+y2/3=a2/3. Then the length of the segment of the tangent between the coordinate axes in of length
View SolutionLet P be any point on the curve x2/3+y2/3=a2/3. Then the length of the segment of the tangent between the coordinate axes in of length
View SolutionWrite the coordinates of the point at which the tangent to the curve y=2x2−x+1 is parallel to the line y=3x+9 .
View SolutionFind the coordinates of the point on the curve y2=3−4x where tangent is parallel to the line 2x+y−2=0 .
View SolutionLet P be the point on the parabola y2=4x which is at the shortest distance from the center S of the circle x2+y2−4x−16y+64=0. Let Q be the point on the circle dividing the line segment SP internally. Then
View SolutionFind the co-ordinates of the point of intersection of tangents at the points where the line 2x+y+12=0 meets the circle x2+y2−4x+3y−1=0
View SolutionThe lines 2x−5y+1=0 and 10x−4y−3=0 meets the coordinate axes in concylic points, then equation to the circle is
View SolutionFind the coordinates of the point of intersection of tangent at the points where x+4y−14=0 meets the circle x2+y2−2x+3y−5=0
View SolutionThe straight line x−2y+5=0 intersects the circle x2+y2=25 in points P and Q, the coordinates of the point of the intersection of tangents drawn at P and Q to the circle is
View Solution
