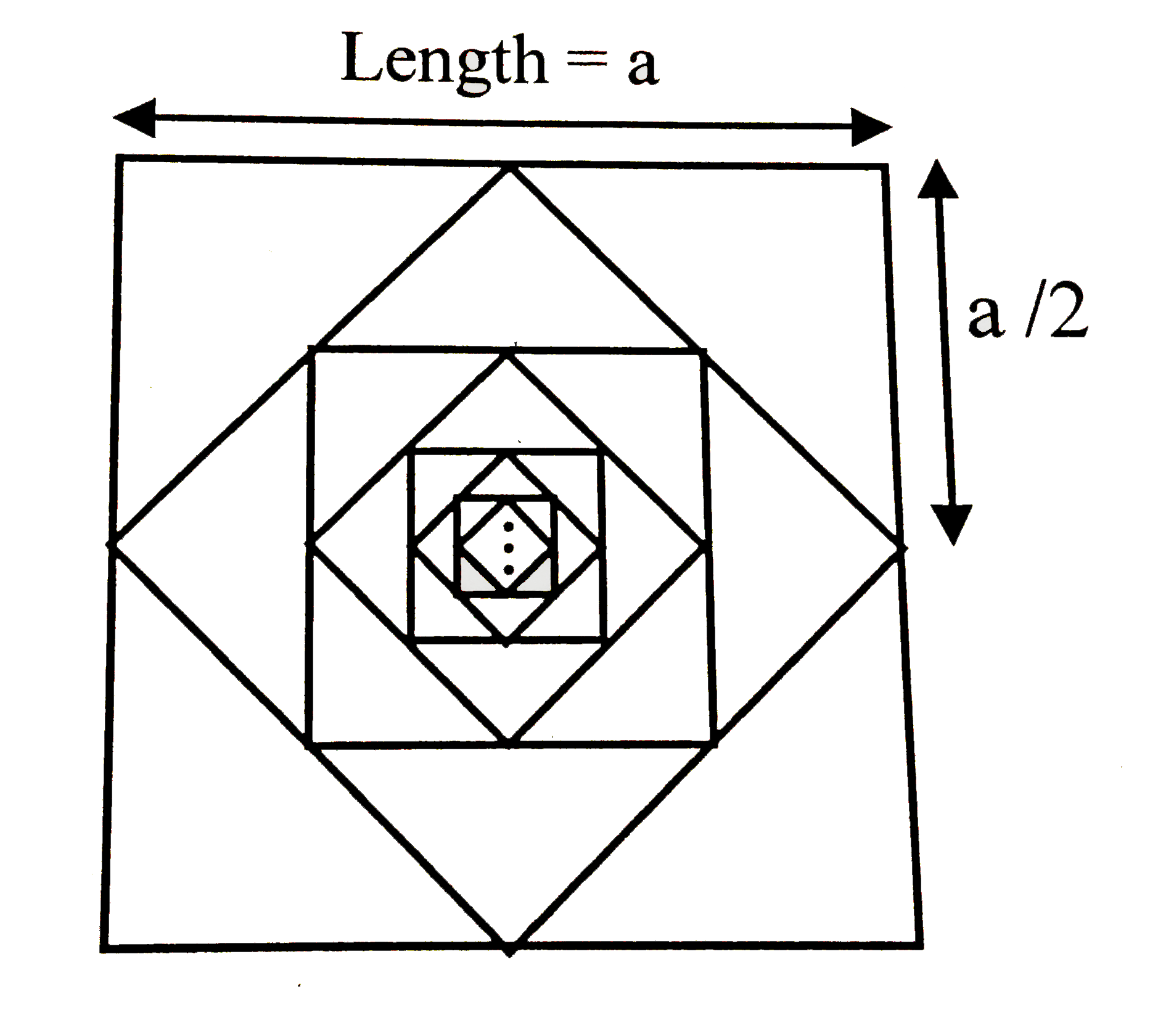
Let S(1) be the sum of areas of the squares whose sides are parallel t

The sum of the squares of three distinct real
numbers which are in GP is $S^{2}$ , if their sum is $α S$ , then
A $1 < α^{2} < 3$
B $\frac{1}{3} < α^{2} < 1$
C $1 < α < 3$
D $\frac{1}{3} < α < 1$
Let A be the area of a square whose each side is 10 cm. Let B be the area of the square whose diagonals are 14 cm each. Then (A-B) is equal to
A0
B1
C2
D4
3 point O $(0, 0), P (a, a^{2}), Q (- b, b^{2}) (a > 0, b > 0)$ are on the parabola $y = x^{2}$ . Let $S_{1}$ be the area bounded by the line PQ and parabola let $S_{2}$ be the area of the $Δ O P Q$ , the minimum value of $S_{1} / S_{2}$ is
A $2 / 3$
B $5 / 3$
C2
D $73$

Let $S_{1}$ be the sum of areas of the squares whose sides are parallel to coordinates axes
Let $S_{2}$ be the sum of areas of the slanted squares as shown in the figure. Then $S_{1} / S_{2}$ is