Let u(t) and v(t) be two solutions of the differential equation dydt=et2y(t)+sint with u(2)<v(2)
Statement 1: u(t)<v(t) for all t
Statement: u-v is proportional ot a positive function of t.
The correct Answer is:a
Topper's Solved these Questions
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONS EXERCISE - Questions from Previous Years. AIEEE/JEE Main Papers38videos
DIFFERENTIAL EQUATIONS
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - DIFFERENTIABILITY AND DIFFERENTIATION EXERCISE - Questions from Previous Years. B-Architecture Entrance Examination Papers16videos
DIFFERENTIABILITY AND DIFFERENTIATION
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - ELLIPSEEXERCISE - Previous Years B-Architecture Entrance Examination Papers6videos
ELLIPSE
Similar Questions
Let u(t)andv(t) be two solutions of the differential equation (dydt)=et2y+sint with u(2)<v(2). Statement-1 : u(2)<v(2) for all t. Statement-1 : u−v is proportional to a positive function of t.
View SolutionLet I be the purchase value of an equipment and V(t) be the value after it has been used for t years. The value V(t) depreciates at a rate given by differential equation (dVtdt=−k(T−t) , where k>0 is a constant and T is the total life in years of the equipment. Then the scrap value V(T) of the equipment is : (1) T2−1k (2) I−kT22 (3) I−k(T−t)22 (4) e−kT
View Solution
Knowledge Check
- Question 1 - Select One
The figure shows the variation of V with i at temperatures T1 and T2. Then T1−T2 is proportional to
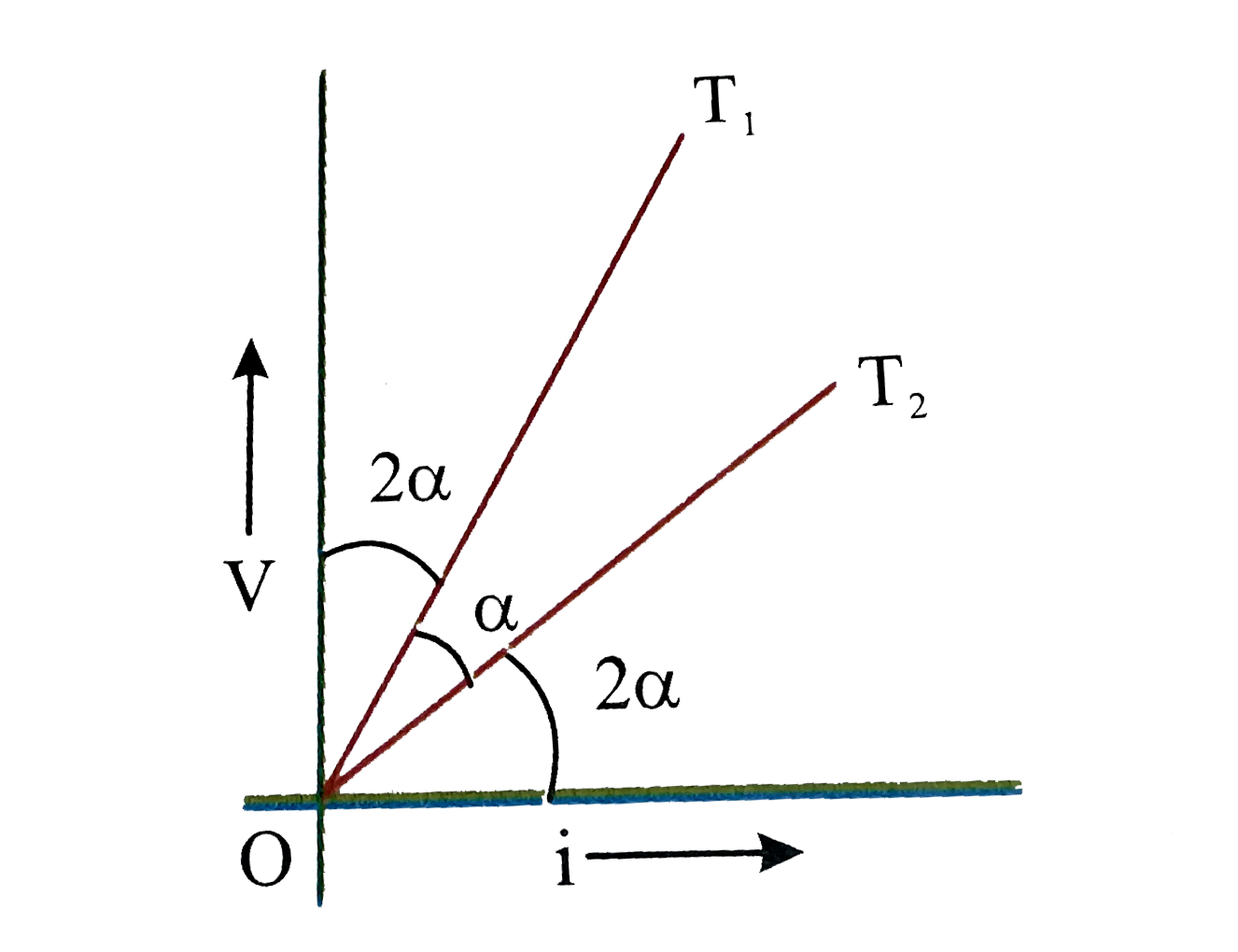 Atan2αBtanαCsinαDcos2α
Atan2αBtanαCsinαDcos2α - Question 2 - Select One
The orthocentre of the triangle formed by the lines y=0,(1+t)x−ty+t(1+t)=0 and (1+u)x−uy+u(1+u)=0(t≠u) for all values of t and u lies on the line.
Ax−y=0Bx+y=0Cx−y+1=0Dx+y+1=0
Let I be the purchase value of an equipment and V(t) be the value after it has been used for t years. The value V(t) depreciates at a rate given by differential equation (dVtdt=−k(T−t) , where k>0 is a constant and T is the total life in years of the equipment. Then the scrap value V(T) of the equipment is :
(1) T2−1k
(2) I−kT22
(3) I−k(T−t)22
(4) e−kTView SolutionLet I be the purchase value of an equipment and V(t) be the value after it has been used for t years. The value V(t) depreciates at a rate given by differential equation dV(t)dt=-k(T-t) , where k>0 is a constant and T is the total life in years of the equipment. Then the scrap value V(T) of the equipment is : (1) T2−1k (2) I−kT22 (3) I−k(T−t)22 (4) e−kT
View Solutionconsider a head on collision between two particles of masses m1andm2. The initial speeds of the particles are u1andu2 in the same direction. The collision starts at t=0 and the particles interact for a time interval △t. during the collision the speed of the first particle varies as
v(t)=u1+t/ t(v1−u1) Find the speed of the second particle as as function of time during the collision.View SolutionIf u+t=5 and u-t=2 , what is the value of (u−t)(u2−t2) ?
View SolutionConsider the differential equation dudt=sin(t+u)+cos(t+u). The general solution of the equation is log (t,u) = t + c.
The value of [f(0,2π3)], where [.]
represents the greatest integer function, is equal toView SolutionDifferentiate the following w.r.t. x or t or u as the case may be:
10. z=uu2+1View Solution

