Let X denote the number of hours you study during a randomly selected school day The probability that X can take the values x. has the following form, where k is some unknown constant. P(X=x)={0. 1 if x=0,k x if x=1 , 2k(5-x) if x=3 or 4, 0 otherwise
Step by step video & image solution for Let X denote the number of hours you study during a randomly selected school day The probability that X can take the values x. has the following form, where k is some unknown constant. P(X=x)={0. 1 if x=0,k x if x=1 , 2k(5-x) if x=3 or 4, 0 otherwise by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Let X denote the number of hours you study during a randomly selected school day. The probability that X take the values of x has the following form, where k is some unknown constant. P(X=x)={(0.1ifx=0),(kx,ifx=1or2),(k(5−x),ifx=3or4),(0,otherwise)
Find:
(i) k
(ii) the probability that you study exactly two hours,
(iii) the probability that you study at most two hours.
View SolutionLet X denote the no. of hours you study during a randomly selected school day. The probability that X can take the values x, has the following form, where λ is some unknown constant.
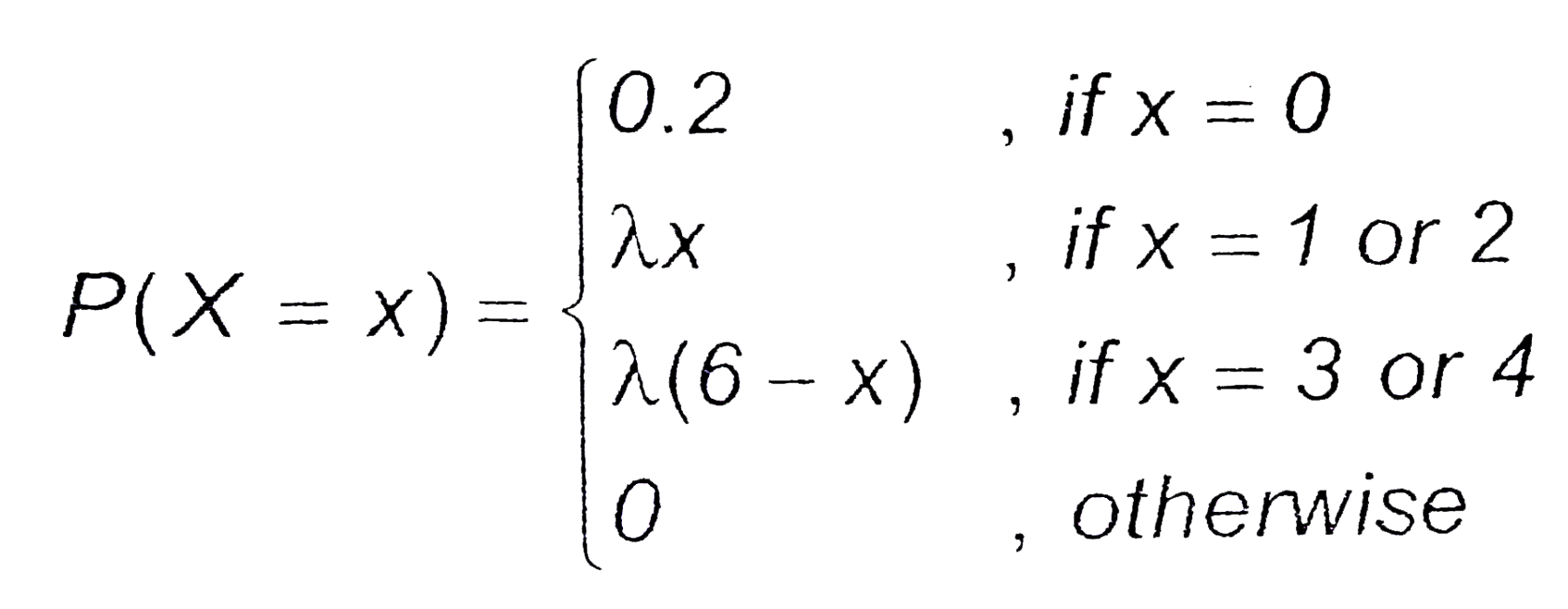
(a) Find the value of λ
(b) What is the probability that you study at least two hours ? Exactly two hours? At most two hours?
View SolutionLet, X denote the number of colleges where you will apply after your results and P (X = x) denotes your probability of getting admission in x number of colleges. It is given that P(X=x)={kx;ifx=0or1, 2kx;ifx=2,k(5−x), ifx=3or4, 0;ifx>4 where k is a positive constant. Find the value of k . Also find the probability that you will get admission in (i) exactly one college (ii) at most 2 colleges (iii) at least 2 colleges.
View SolutionThe random variable X has a probability distribution P(X) of the following form, where k is some number : P(X) = {(k,ifx=0),(2k,ifx=1),(3k,ifx=2),(0otherwise) (a) Determine k. (b) Find P (X<2) , P (X≤2) , P(X≥2)
View SolutionA random variable X takes the values 0,1,2,3,..., with prbability PX(=x)=k(x+1)(15)x, where k is a constant, then P(X=0) is.
View SolutionFor what value of k is the function f(x)={sin5x3x, if x≠0, k, if x=0 continuous at x=0 ?
View SolutionFind the value of the constant k so that the given function is continuous at the indicated point: f(x)={1−cos2kxx2ifx≠08ifx=0 at x=0
View SolutionFind the value of the constant k so that the given function is continuous at the indicated point: f(x)={k(x2+2), if x≤03x+1, if x>0 at x=0 .
View SolutionDetermine the value of the constant k so that the function f(x)={sin2x5x, if x≠0 ,k if x=0 is continuous at x=0 .
View SolutionThe random variable X has a probability distribution P(X) of the following form, where k is some arbitary real number:
P(X=x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩k,if x=02k,if x=13k,if x=20,otherwise
(i) Determine the value of k (ii) Find P(X<2),P(X≤2),P(X≥2)
View Solution
