Let z∈C and if A={z:arg(z)=π4}and B={z:arg(z−3−3i)=2π3}. Then n(A⌢B)=
A
1
B
2
C
3
D
0
Text Solution
The correct Answer is:D
(d) A={z,arg(z)=π4}
z lies on the ray from origin (excluding origin) at an angle π/4 with positive real axis.
B={z,arg(z−3−3i)=2π3}
z lies on the ray from 3+3i(excluding 3+3i) at an angle 2π/3 with positive real axis.
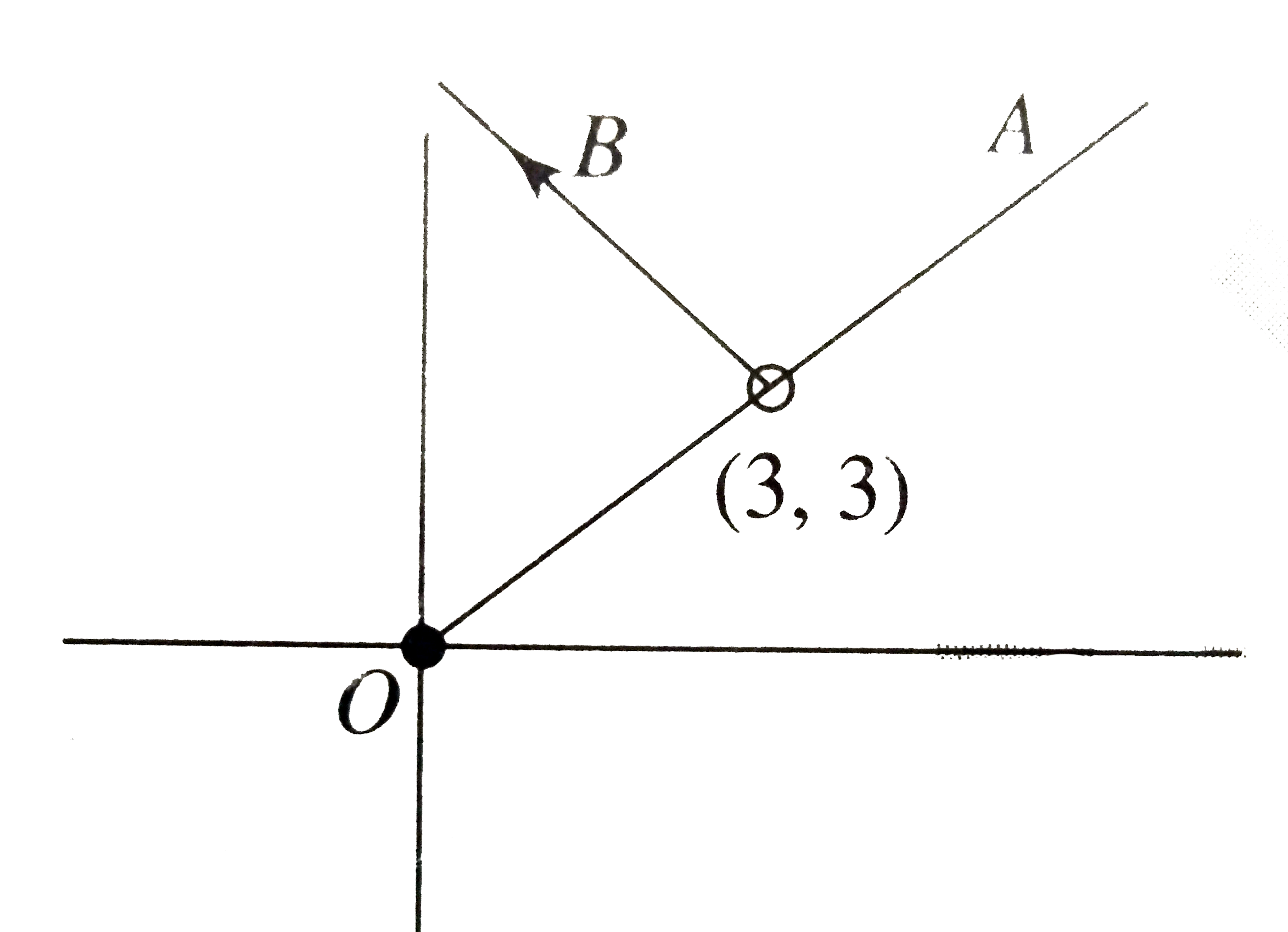
We can observe that 3+3i∈A but ≠B
∴n(A∩B)=0
|
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Multiple Correct Answer
11 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column
1 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
- CONIC SECTIONSBOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises
87 Videos
Similar Questions
Knowledge Check
If arg(z+a)=π6 and arg(z−a)=2π3(a∈R+), then
A|z|=aB|z|=2aCarg(z)=π3Darg(z)=π2If arg(z+a)=π/6andarg(z−a)=2π/3(a∈R+), then
A|z|=aB|z|=2aCarg(z)=π2Darg(z)=π3
Find the complex number z if arg(z+1)=π6 and arg(z−1)=2π3
View SolutionNumber of z, which satisfy Arg(z−3−2i)=π6 and Arg(z−3−4i)=2π3 is/are :
View SolutionIf |z| = 6 and arg(z) =3π4, find z.
View SolutionLet A(z1) be the point of intersection of curves arg(z−2+i)=3π4)andarg(z+i√3)=π3,B(z2) be the point on the curve arg(z+i√3)=π3such that |z2−5|=3 is minimum and C(z2) be the centre of circle |z−5|=3. The area of triangle ABC is equal to
View SolutionThe area bounded by the curves argz=π3andargz=2π3andarg(z−2−2i√3)=π in the argand plane is (in sq. units)
View SolutionIf z=a+ib satisfies arg(z−1)=arg(z+3i), then (a−1):b=
View Solution
