z1, z2, z3 are vertices of a triangle. Match the condition in List I with type of triangle in List II.
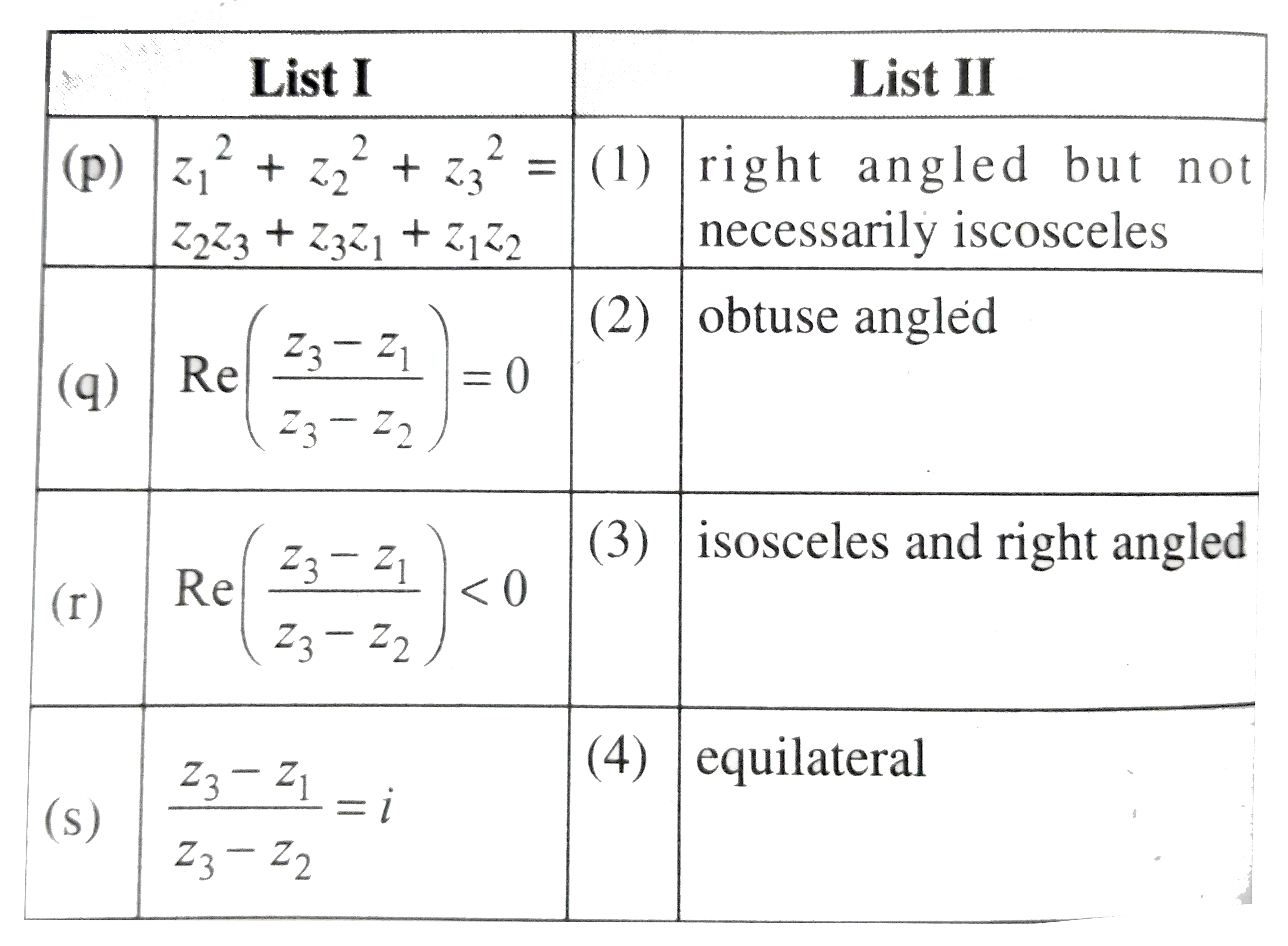
Codes
A
pqrs3214
B
pqrs1243
C
pqrs4123
D
pqrs2143
Text Solution
The correct Answer is:C
(c) (p) Standard condition of equilateral triangle.
(q)Re(z3−z1z3−z2)=0⇒arg(z3−z1z3−z2)=±π2
⇒ Triangle is right angled.
(r)Re(z3−z1z3−z2)<0⇒arg(z3−z1z3−z2)>π2
(s)z3−z1z3−z1=i=eiπ2 and |z3−z1|=|z3−z2|⇒ triangle is isosceles and right angled.
|
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Comprehension
11 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Examples
125 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Multiple Correct Answer
11 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
- CONIC SECTIONSBOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises
87 Videos
Similar Questions
Knowledge Check
If z1,z2,z3 represent the vertices of a triangle, then the centroid of the triangle is given by
Aaz1+bz2+cz3a+b+cBz1+z2+z33Cz1z2z33Dnone of theseThe complex numbers z1,z2,z3 are the vertices of a triangle . Then the complex numbers z which make the triangle into a parallelogram is
Az1+z2−z3Bz2+z3−z1Cz3+z1−z2DnoneIf z1,z2,z3 are the vertices of an isoscles triangle right angled at z2, then
Az21+2z22+z23=2z2(z1+z3)Bz21+z22+z23=2z2(z1+z3)Cz21+z22+2z23=2z2(z1+z3)D2z21+z22+z23=2z2(z1+z3)
The complex number z1z2z3 are the vertices of a triangle .Then the complex number z which make the triangle into parallelogram is
View SolutionIf the points z1,z2,z3 are the vertices of an equilateral triangle in the Argand plane, then which one of the following is not correct?
View SolutionIf z1,z2,z3 be vertices of an equilateral triangle occurig in the anticlockwise sense, then
View SolutionIf the points z1,z2,z3 are the vertices of an equilateral triangle in the Argand plane, then which one of the following is not correct?
View SolutionIf z1,z2,z3 be vertices of an equilateral triangle occurig in the anticlockwise sense, then
View Solution

