Like the adjoining figure, draw two circles with centres C and D which intersect each other at the points A and B . Draw a straight line through A which intersects the circle C at the point P and the circle with centre D at the point Q. Prove that (i) ∠PBQ=∠CAD(ii)∠BPC=∠BQD.
The correct Answer is:(i)∴segAP∣∣segBQ (ii) ∴ΔAPR~ΔRQB (iii) ∴∠RQB=110∘
Step by step video & image solution for Like the adjoining figure, draw two circles with centres C and D which intersect each other at the points A and B . Draw a straight line through A which intersects the circle C at the point P and the circle with centre D at the point Q. Prove that (i) angle PBQ= angle CAD (ii) angle BPC= angle BQD. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Practice Set 3.33videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Practice Set 3.46videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Practice Set 3.14videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - Chapter 6: Statistics4videos
CHALLENGING QUESTIONS
- BOOK - TARGET PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - CHAPTER ASSESSMENT19videos
CO-ORDINATE GEOMETRY
Similar Questions
Two circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View SolutionIn the figure, two circles with centers O and P intersect each other at points D and C. Line AB intersects the circle with centre O at points A and B and touches the circle with centre P at point E. Prove ∠ADE+∠BCE=180∘.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two circles intersect each other at the points A and B, A straight line parallel to AB intersects the circles at C, D, E and F. If CD = 4.5 cm, then the measure of EF is
A1.50cmB2.25cmC4.50cmD9.00cm
In figure, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points B and D intersect each other at point C. Prove that □ ABCD is cyclic.
 View Solution
View SolutionTwo circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that :∠ADC+∠BCD=180∘
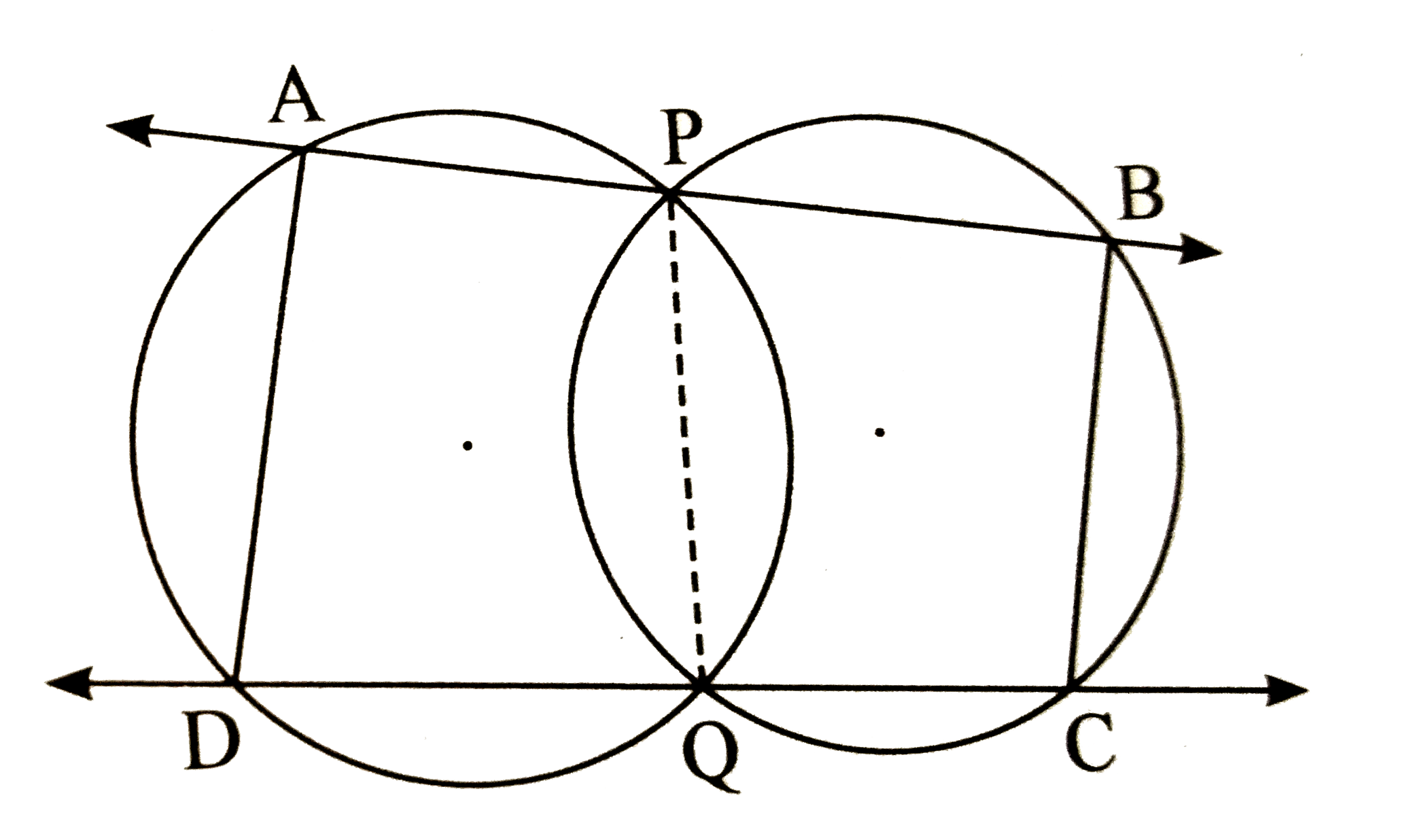 View Solution
View SolutionIn the circle with centre O and A,B,C are the points on the circle, ∠AOB=60∘. Find ∠ACB
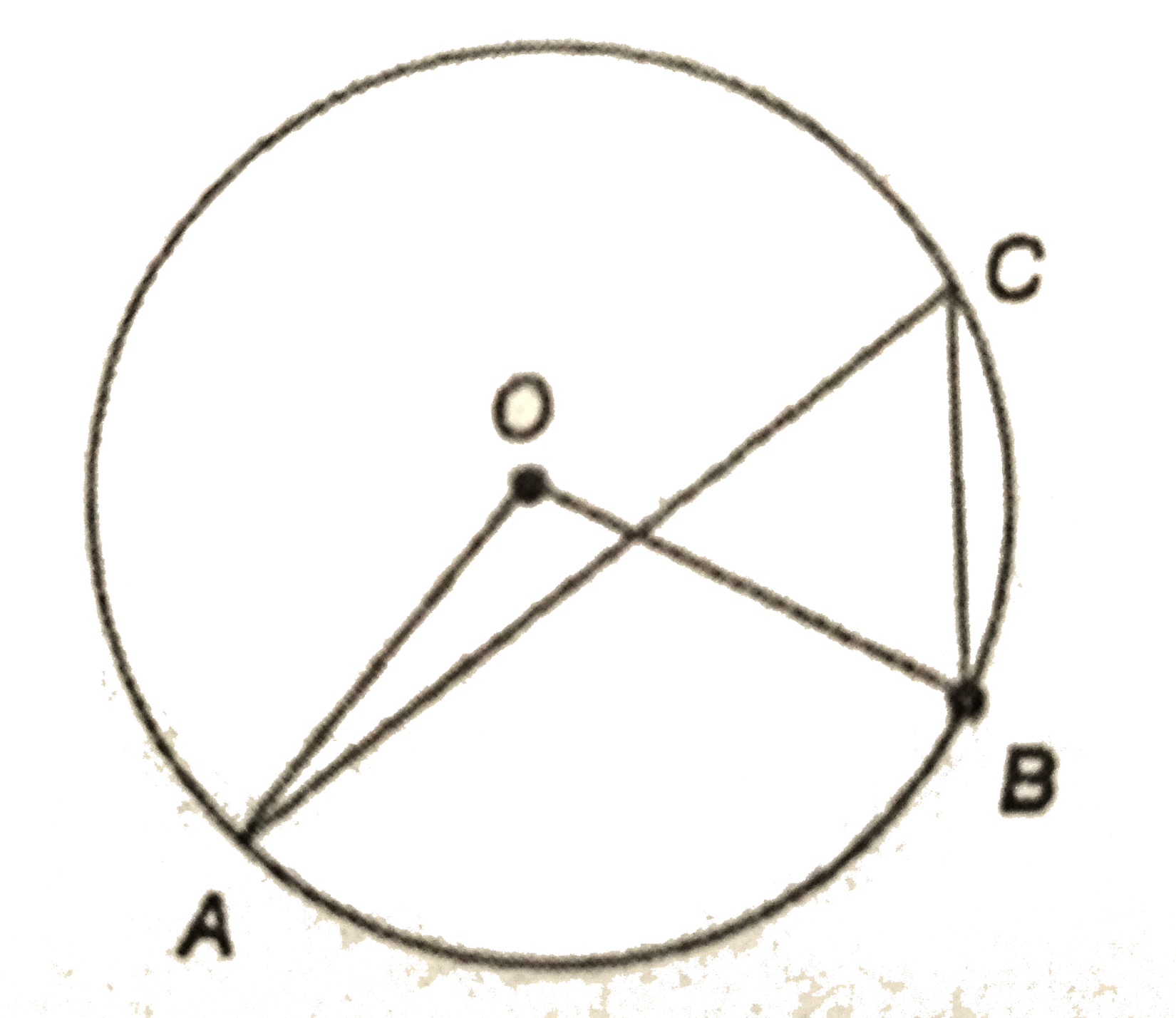 View Solution
View SolutionTwo circle with centres A and B intersect at C and D. Prove that ∠ACB=∠ADB.
View SolutionIn the adjoining figure , circles with centres C and D touch internally at point E. D lies on the inner circle. Chord EB of the other circle intersects innet circle at point A. Prove that, seg EA≅seg AB.
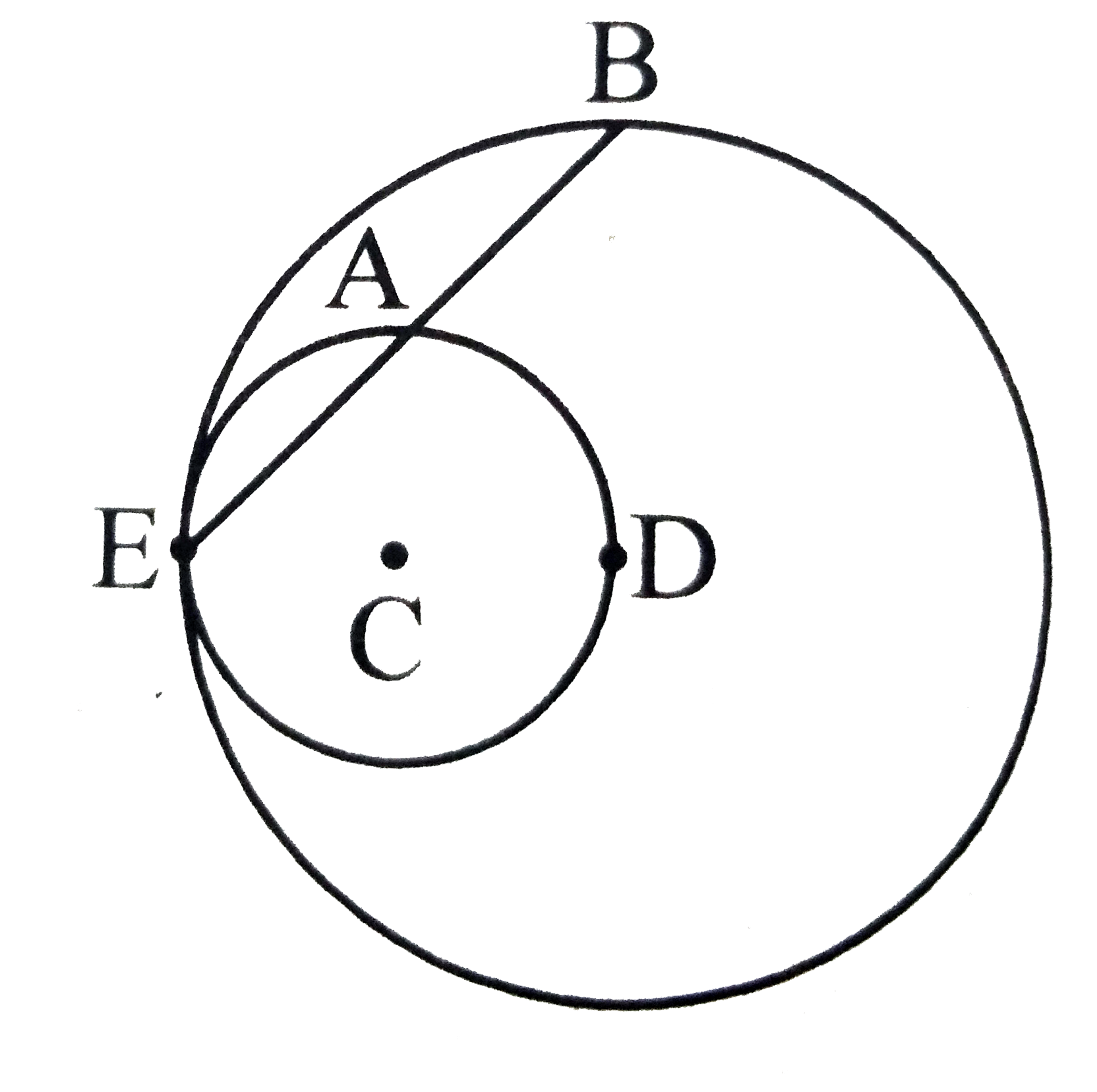 View Solution
View Solution
A line which intersect the circle at two points (P and Q) is called a.................. of the circle.View SolutionTwo equal circles intersect in P and Q . A straight line through P meets the circles in A and B . Prove that QA=QB.
View Solution

