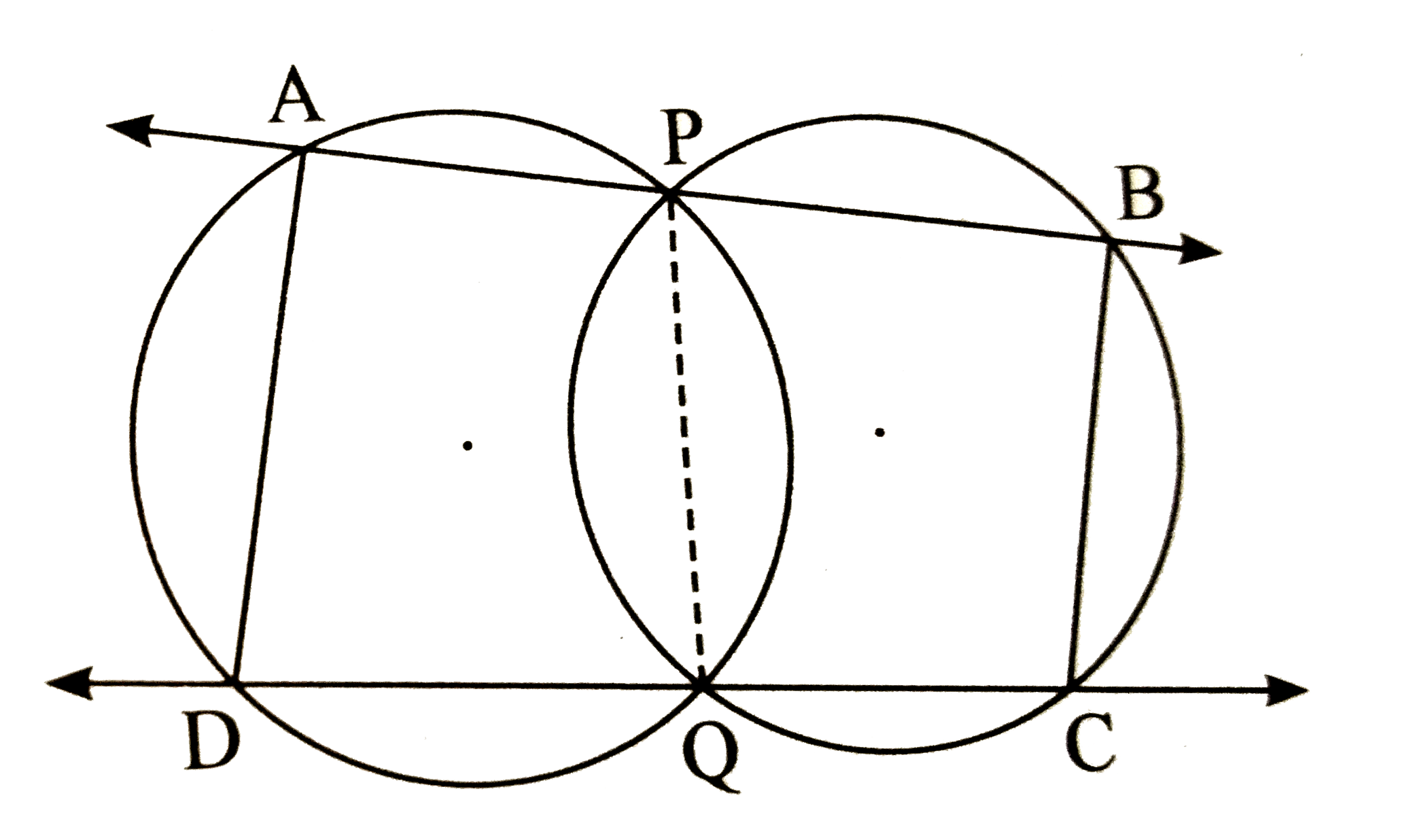
In figure, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points B and D intersect each other at point C. Prove that □ ABCD is cyclic.

The correct Answer is:∴□ ABCD is cyclic ……….( Converse of cyclic quadrilateral theorem )
Step by step video & image solution for In figure, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points B and D intersect each other at point C. Prove that square ABCD is cyclic. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - Challenging Questions
10 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.5
6 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
1 Videos
- COORDINATE GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.5
13 Videos
Similar Questions
In figure, two circles intersect each other at points S and R. Their common tangent PQ touches the circle at points P,Q. Prove that, ∠PRQ+∠PSQ=180∘.

View SolutionTwo circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that :∠ADC+∠BCD=180∘
View Solution
Knowledge Check
Two circles intersect each other at the points A and B, A straight line parallel to AB intersects the circles at C, D, E and F. If CD = 4.5 cm, then the measure of EF is
A1.50cmB2.25cmC4.50cmD9.00cm
Two circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.

View SolutionIn figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R,S and P,Q respectively. Prove that : seg SQ || seg RP.

View SolutionIn the figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R,S and P,Q respectively. Prove that : seg SQ ∣∣ seg RP.

View SolutionIn the figure, two circles intersect each other at points A and B. AP and AQ are the diameters of these circles. Prove that PBQ is a straight line.

View SolutionIn the figure, two circles with centers O and P intersect each other at points D and C. Line AB intersects the circle with centre O at points A and B and touches the circle with centre P at point E. Prove ∠ADE+∠BCE=180∘.

View SolutionTwo circles intersect each other at point P an Q. If PA and PB are two diameter then find ∠AQB.
View Solution
