limn→∞n∑r=1rn2+n+4 equals
a. 0
b. 1/3
c. 1/2
d.1Solution in Punjabi
(a) 14sin4+115cos4−116
(b) 14sin4−116cos4+116
(c) 116(1−sin4)
(d) 116(1−cos4)
The correct Answer is:D
Step by step video & image solution for lim_(nto oo)sum_(r=1)^(n)r/(n^(2)+n+4) equalsa. 0b. 1/3c. 1/2d.1 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise (More Than One Correct Option Type Questions)15videos
LIMITS
- BOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise (Passage Based Questions)10videos
LIMITS
- BOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - SOLVED EXAMPLES1videos
LIMITS
- BOOK - ARIHANT MATHSCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)8videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - ARIHANT MATHSCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)4videos
LOGARITHM AND THEIR PROPERTIES
Similar Questions
If limx→∞4x(π4−tan−1(x+1x+2))=y2+4y+5 then y can be equal to
05:20View SolutionIf limx→af(x)=1 and limx→ag(x)=∞ then limx→a{f(x)}g(x)=elimx→a(f(x)−1)g(x)
limx→0(sinxx)sinxx−sinx is equal to06:28View SolutionTo evaluate limx→a[f(x)], we must analyse the f(x) in right hand neighbourhood as well as in left hand neighbourhood of x=a. E.g. In case of continuous function, we may come across followign cases.
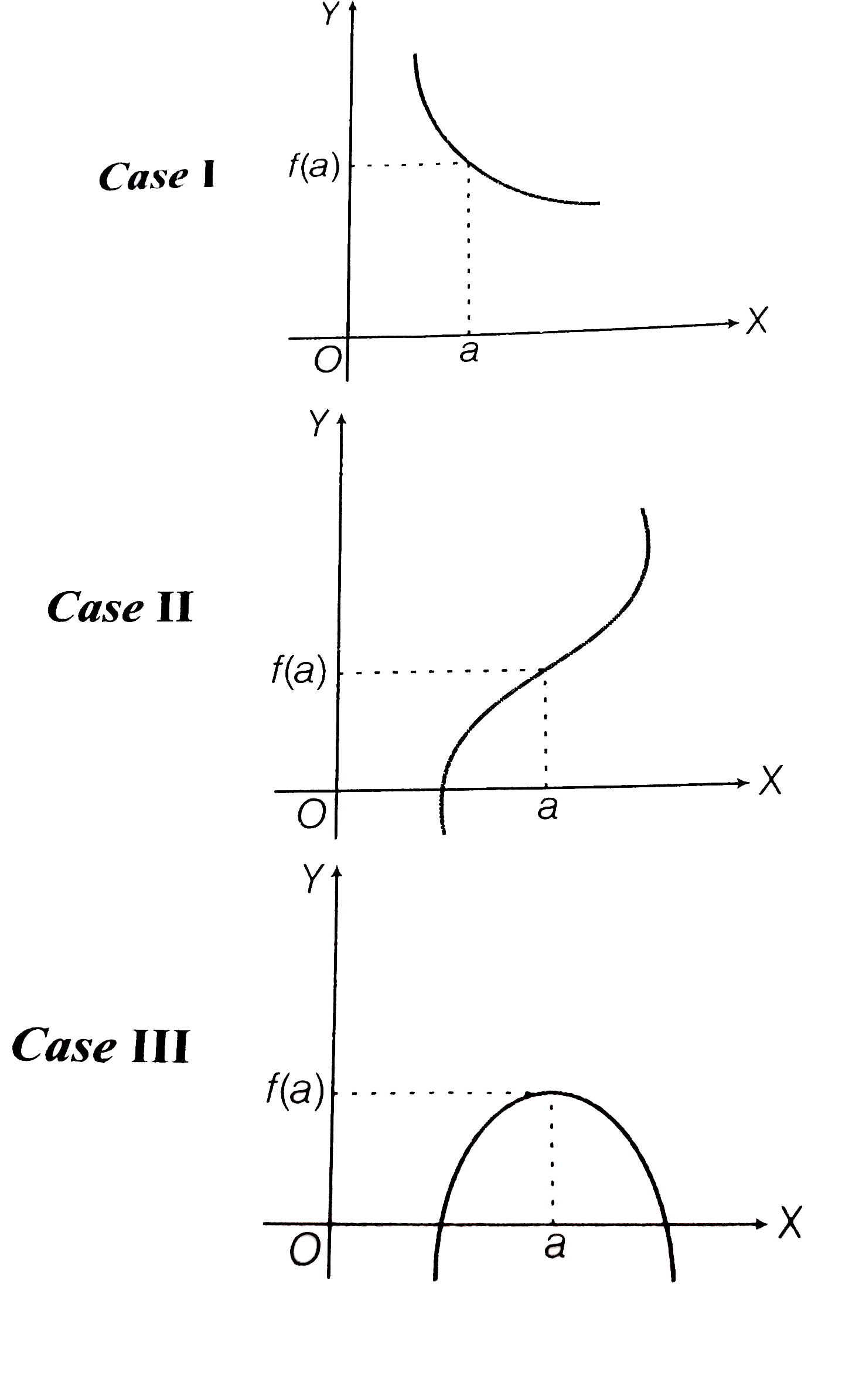
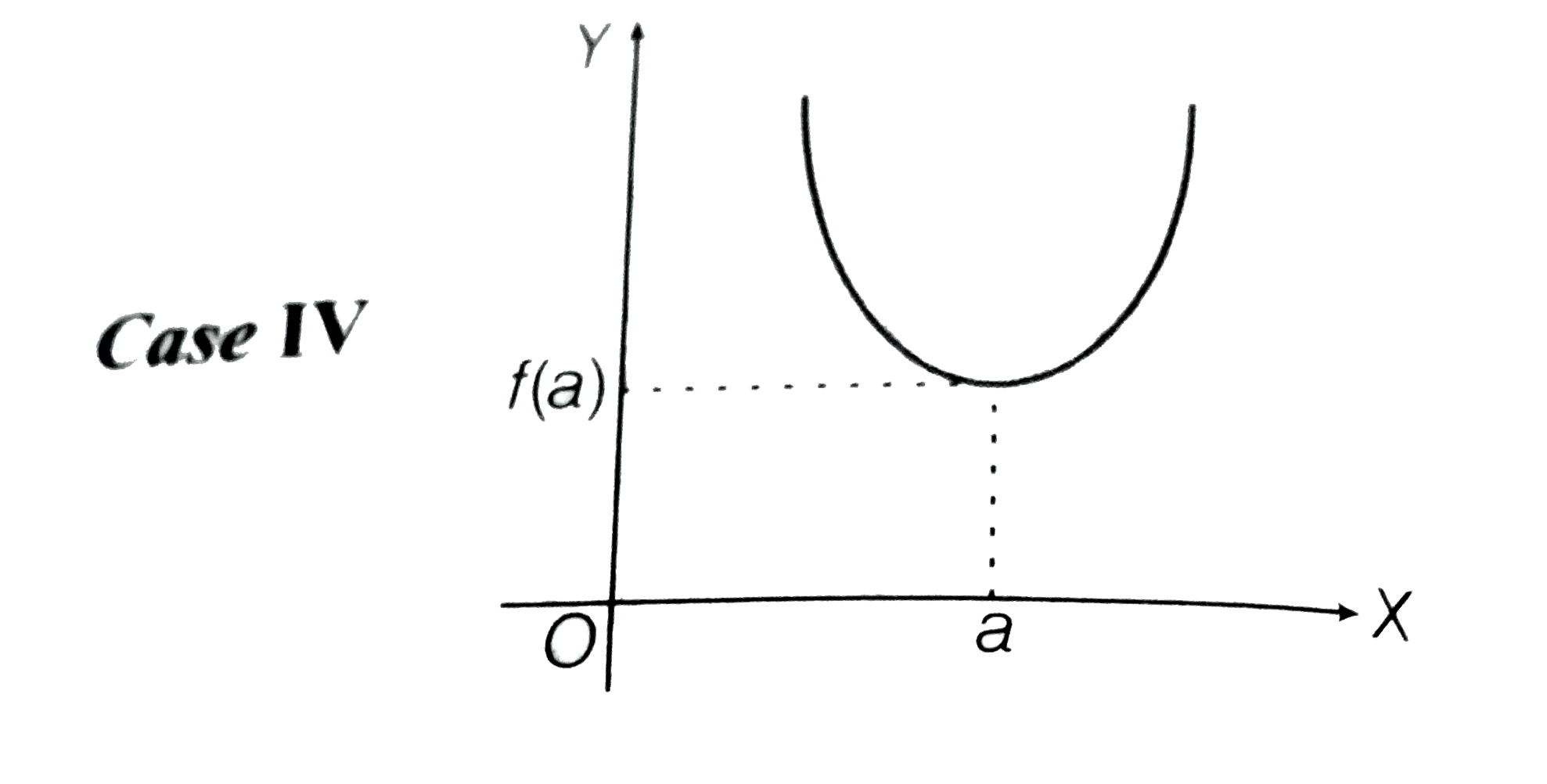
Iff(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II. If f(a) is not an integer, the limit exists in all the cases. ltbgt If f'(1)=−3 and limx→1[f(x)−12] does not exist, (where [.] denotes the greatest integer function), then03:19View SolutionIf α=3sin−1(611andβ=3cos−1(49), where the inverse trigonometric functions take only the principal values, then the correct options (s) is (are)
02:11View SolutionIn Which quadrant Point (−2,−3) will be lie.
02:21View SolutionIf sum_(r=0)^(2n)a_(r)(x-100)^(r)=sum_(r=0)^(2n)br(x-101)^(r) and a_(k)=(2^(k))/(kC_(n))AA k>=n then b_(-) n equals ( A )2^(n)(2^(n+1)-1)(B)2^(n)(2^(n)-1)(C)2^(n)(2^(n)+1)(D)2^(n+1)(2^(n)-1)
03:47View SolutionThe value of lim_(n rarr oo)(1*sum_(r=1)^(n)(r)+2*sum_(r=1)^(n-1)(r)+3sum_(r=1)^(n-2)(r)+....+n.1)/(n^(4))
05:02View Solutionlim_ (n rarr oo) (1) / (n ^ (4)) sum_ (r = 1) ^ (n) r (r + 2) (r + 4) =
02:35View Solutionlimn→∞1n2n∑r=1rer/n=
07:59View Solutionlimn→∞n∑r=1rn2+n+4 equals
02:03View Solutionn∑r=1(ar+br),a,b∈R+ is equal to :
02:08View Solutionlimn→∞1n2n∑r=1r√n2+r2 बराबर है
02:34View Solutionlimn→∞1n2n∑r=1rer/n equals :
View SolutionIf n∑r=1Tr=n(n+1)(n+2)(n+3)12 then 4(limx→∞n∑x−11Tr) is equal to
02:06View SolutionIf f(x) is integrable over [1,2] then ∫21f(x)dx is equal to (a) limn→∞1nn∑r=1f(rn) (b) limn→∞1n2n∑r=n+1f(rn) (c) limn→∞1nn∑r=1f(r+nn) (d) limn→∞1n2n∑r=1f(rn)
02:19View Solutionlimn→∞n∑r=1rn2+n+4 equals
02:31View Solution
