(where denotes the greatest integer function) is
-1
1
0
2
The correct Answer is:B
or
=[a value slightly lesser than 7]
Topper's Solved these Questions
- LIMITSBOOK - CENGAGECHAPTER - LIMITSEXERCISE - Exercise (Multiple)
18 Videos
- LIMITSBOOK - CENGAGECHAPTER - LIMITSEXERCISE - Exercise (Comprehension)
20 Videos
- LIMITSBOOK - CENGAGECHAPTER - LIMITSEXERCISE - Exercise 2.8
8 Videos
- JEE 2019BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 10
9 Videos
- LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSBOOK - CENGAGECHAPTER - LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSEXERCISE - DPP 1.2
10 Videos
Similar Questions
(lim)x→0[min(y2−4y+11)sinxx](where[.]de¬esthe greatest integer function is 5 (b) 6 (c) 7 (d) does not exist
View SolutionTo evaluate limx→a[f(x)], we must analyse the f(x) in right hand neighbourhood as well as in left hand neighbourhood of x=a. E.g. In case of continuous function, we may come across followign cases.
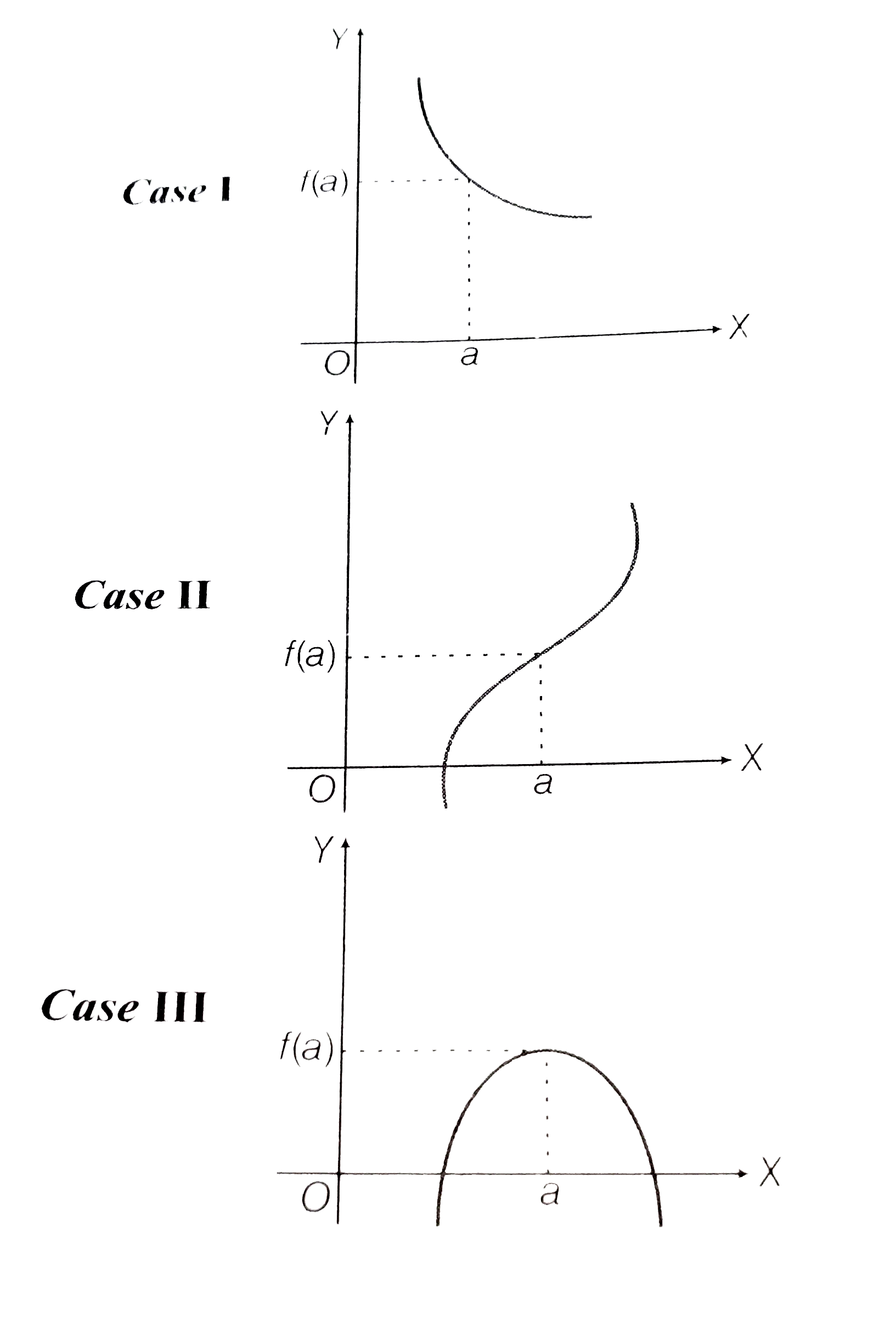
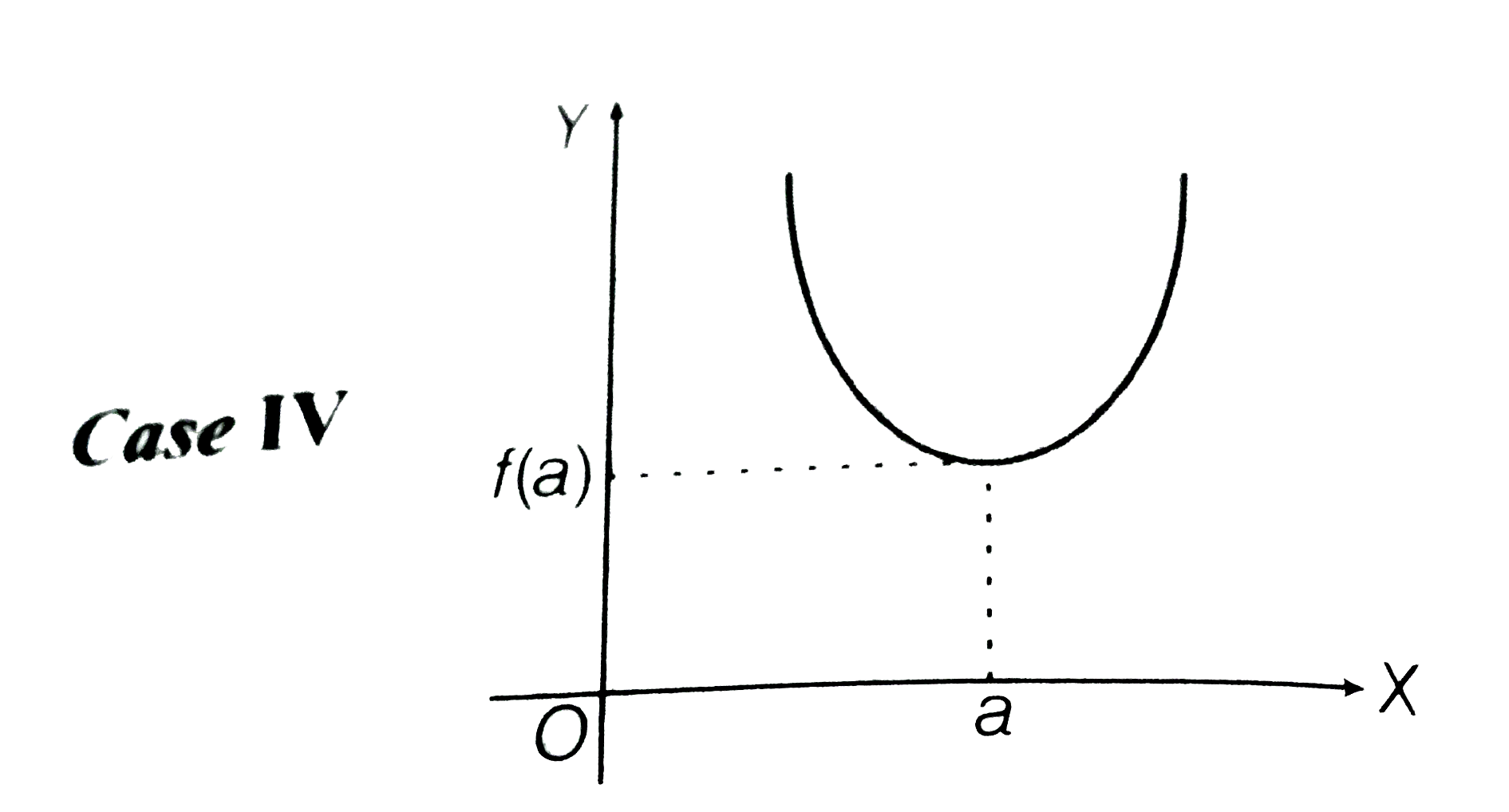
Iff(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II.limx→0[(1−ex).sinx|x|] (where [.] denotes the greatest integer function) equals
View Solution
Knowledge Check
limx→0[(1−ex)sinx|x|] is (where [.] represents the greatest integer function )
A1B2C3Dnone of theselimx→0[sin(sgn(x))(sgn(x))], where [.] denotes the greatest integer function, is equal to
A^(2n)pnB^(2n)CnC(2n)!Dnone of theselimx→0[−2xtanx], where [.] denotes greatest integer function is
A-1B4C5DNone of these
limx→0[sin[x−3][x−3]] where [.] denotes greatest integer function is
View Solutionlimx→−1([x]+|x|). (where [.] denotes the greatest integer function)
View Solutionlimx→0−[x]x (where [.] denotes greatest integer function) is
View SolutionThe value of limx→0sin[x][x] (where [.] denotes the greatest integer function) is
View Solutionlimx→1xsin(x−[x])x−1 ,where [.]denotes the greatest integer function, is
View Solution
