limx→1[cosecπx2]1/(1−x) (where [.] represents the greatest integer function) is equal to
0
1
∞
Does not exists
The correct Answer is:B
cosecπx2→1+ when x→1
or[cosecπx2]=1<br>:." ""limit "=1
Topper's Solved these Questions
- LIMITSBOOK - CENGAGECHAPTER - LIMITSEXERCISE - Exercise (Multiple)
18 Videos
- LIMITSBOOK - CENGAGECHAPTER - LIMITSEXERCISE - Exercise (Comprehension)
20 Videos
- LIMITSBOOK - CENGAGECHAPTER - LIMITSEXERCISE - Exercise 2.8
8 Videos
- JEE 2019BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 10
9 Videos
- LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSBOOK - CENGAGECHAPTER - LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSEXERCISE - DPP 1.2
10 Videos
Similar Questions
limx→1[cosecπx2]1(1−x) (where [.] represents the greatest integer function) is equal to
View SolutionTo evaluate limx→a[f(x)], we must analyse the f(x) in right hand neighbourhood as well as in left hand neighbourhood of x=a. E.g. In case of continuous function, we may come across followign cases.

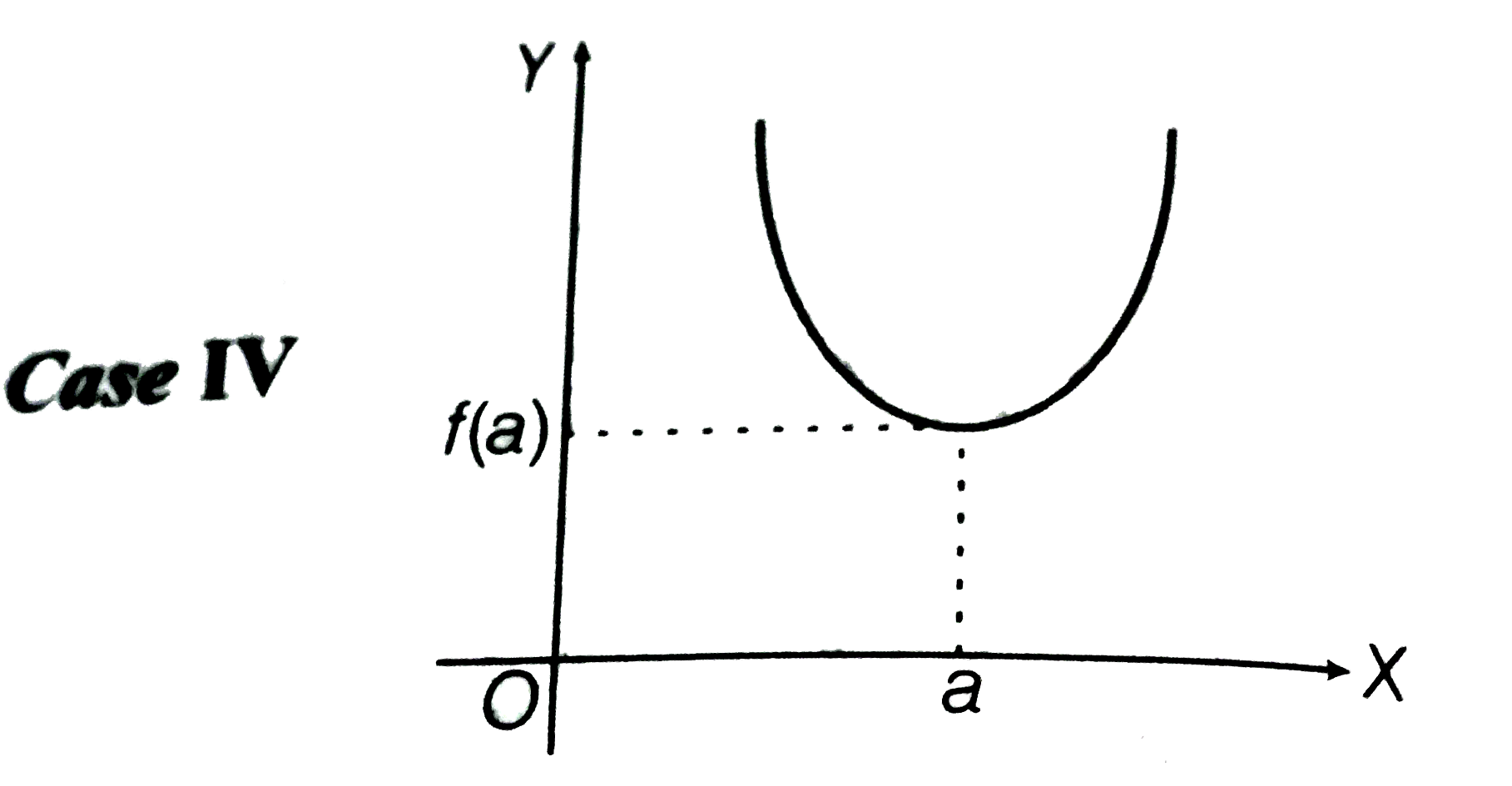
Iff(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II.limx→1[cosecπx2]−1/(1−x) is equal to (where [.] denotes the greatest integer function).
View Solution
Knowledge Check
limx→0[(1−ex)sinx|x|] is (where [.] represents the greatest integer function )
A1B2C3Dnone of theselimx→1[x−1] where [] denotes the greatest integer function is equal to
A1B2C0DDoes not existlimx→0[sin(sgn(x))(sgn(x))], where [.] denotes the greatest integer function, is equal to
A^(2n)pnB^(2n)CnC(2n)!Dnone of these
Find limx→0[x](e1/x−1e1/x+1), (where [.] represents the greatest integer funciton).
View SolutionEvaluate: (lim)x→0tanxx where [.] represents the greatest integer function
View SolutionProve that [limx→0sinxx]=0, where [.] represents the greatest integer function.
View SolutionEvalute [limx→0sin−1xx]=1, where[⋅] represets the greatest interger function.
View Solutionlimx→1+(log√2√2x)1{x} where [ ] represents greatest integer function is
View Solution
