Line L has intercepts aandb on the coordinate axes. When the axes are rotated through a given angle keeping the origin fixed, the same line L has intercepts pandq. Then a2+b2=p2+q2 1a2+1b2=1p2+1q2 a2+p2=b2+q2 (d) 1a2+1p2=1b2+1q2
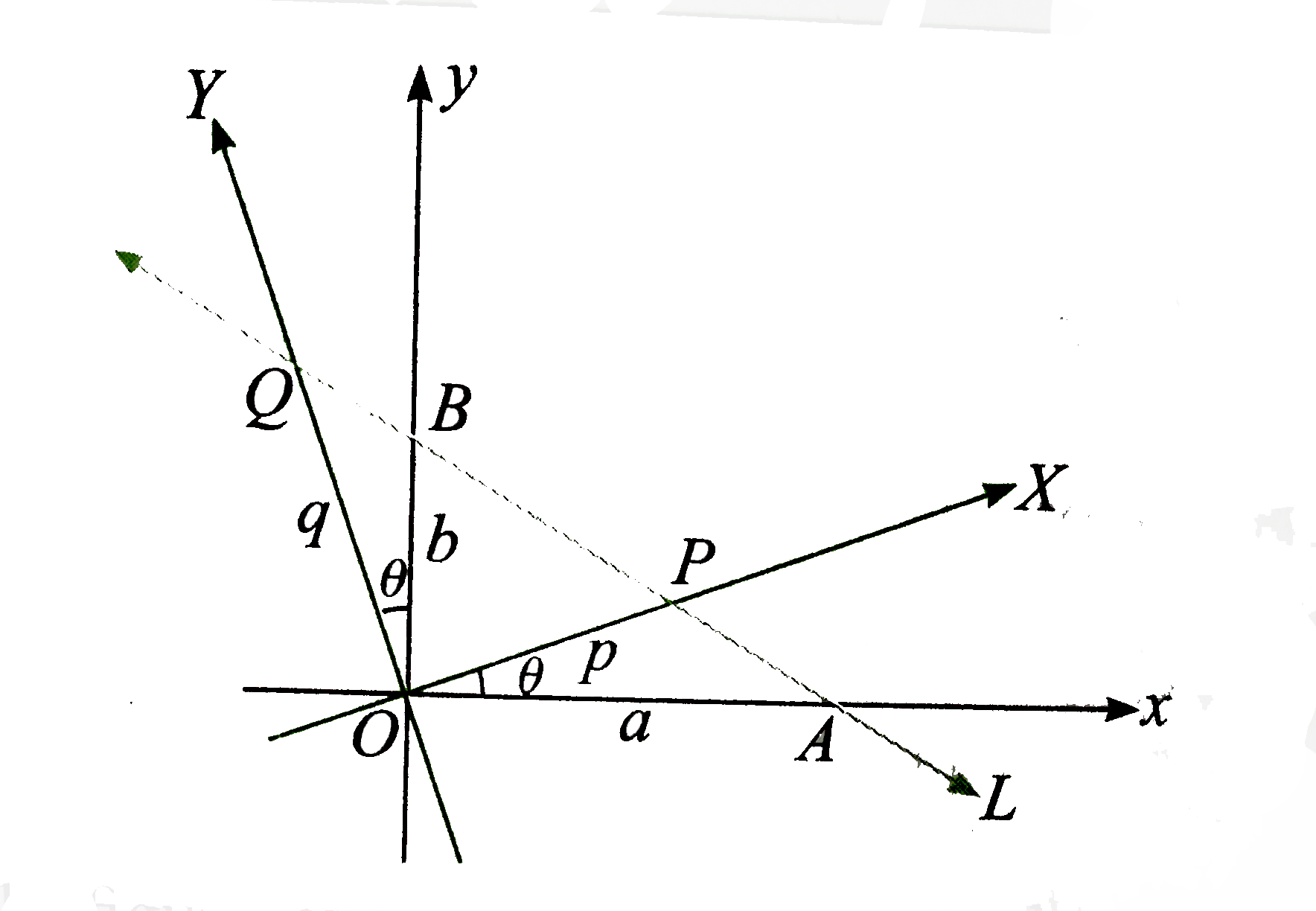
As shown in the figure, axes are rotated by an angle θ about origin in anticlockwise direction.
Line L has intercepts a and b on original axes and intercepts p and q on rotated axes.
Equation of line L w.r.t. original axes is
xa+yb−1=0 (1)
Equation of line L w.r.t. rotated axes is
xp+yq−1=0 (2)
Since origin and line L are not changing their positions, distance of line from origin remains the same even though the axes are rotated.
So, comaring distances of lines given by equations (1) and (2) from origin, we get
∣∣0a+0b−1∣∣√1a2+1b2=∣∣0p+0q−1∣∣√1p2+1q2
⇒1a2+1b2=1p2+1q2
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.1
23 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.2
4 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
Line L has intercepts aandb on the coordinate axes. When the axes are rotated through a given angle keeping the origin fixed, the same line L has intercepts pandq. Then (a) a2+b2=p2+q2 (b)1a2+1b2=1p2+1q2 (c)a2+p2=b2+q2 (d) 1a2+1p2=1b2+1q2
View SolutionLine L has intercepts aandb on the coordinate axes. When the axes are rotated through a given angle keeping the origin fixed, the same line L has intercepts pandq. Then (a) a2+b2=p2+q2 (b)1a2+1b2=1p2+1q2 (c)a2+p2=b2+q2 (d) 1a2+1p2=1b2+1q2
View Solution
Knowledge Check
Line L has intercepts a and b on the coordinate axes. When, the axes area rotated through a given angle, keeping the origin fixed, the same line L has intercepts p and q, then
Aa2+b2=p2+q2B1a2+1b2=1p2+1q2Ca2+p2=b2+q2D1a2+1p2=1b2+1q2The line L has intercepts a and b on the coordinate axes. The coordinate axes are rotated through a fixed angle, keeping the origin fixed. If p and q are the intercepts of the line L on the new axes, then 1a2−1p2+1b2−1q2 is equal to
A−1B0C1Dnone of theseThe line L has intercepts a and b on the coordinate axes. When keeping the origin fixed, the coordinate axes are rotated through a fixed angle,then the same line has intercepts p and q on the rotated axes. Then
Aa2+b2=p2=q2B1a2+1b2=1p2+1q2Ca2+p2=b2=q2D1a2+1p2=1b2+1q2
Line L has intercepts aandb on the coordinate axes. When the axes are rotated through a given angle keeping the origin fixed, the same line L has intercepts pandq. Then (a) a2+b2=p2+q2 (b)1a2+1b2=1p2+1q2 (c)a2+p2=b2+q2 (d) 1a2+1p2=1b2+1q2
View SolutionThu Line L has intercept a and b on the co-ordinate axes. When keeping the origin fixed, the coordinate axis are rotated around a fixed angle, then the line has intercepts p and q on rotate axis, then
View SolutionIf p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then show that 1p2=1a2+1b2.
View SolutionIf p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then show that 1p2=1a2+1b2 .
View SolutionThe line L has intercepts a and b on the coordinate axes. When keeping the origin fixed, the coordinate axes are rotated through a fixed angle,then the same line has intercepts p and q on the rotated axes. Then
View Solution
