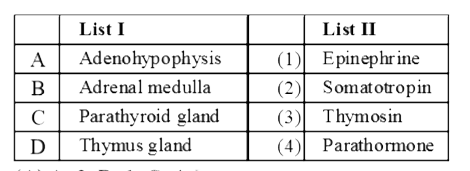
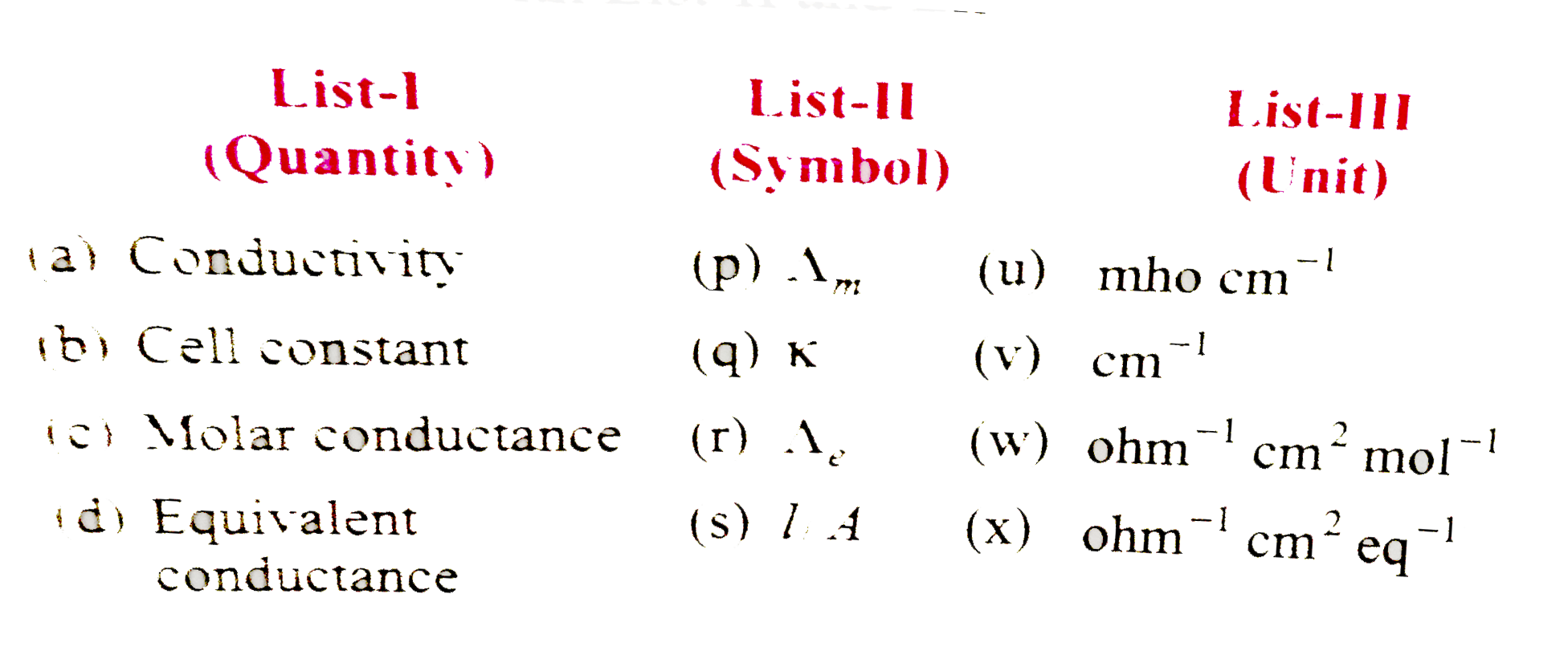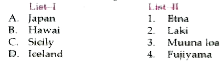List I contains the different sum of the series and List II contains the maximum value of these sums. Match the lists.

Text Solution
The correct Answer is:4
a. 14∑r=0(15−r)r+15!r!(15−r)!.20Cm−r
=14∑r=0(15−r)r+115!r!(15−r)!.20Cm−r
=14∑r=015!(r+1)!(14−r)!.20Cm−r
=14∑r=0.15Cr+1.20Cm−r
=.35Cm+1.
Which has maximum value .35C18.
b. .35C0−.35C1+.35C2−.35C3+.....+(−1)r.35Cr+......
= Coefficient of xr in
(.35C0−.35C1x+.35C2x2−.35C3x3+....+(−1)r.35Cr+....)×(1+x+x2+x3+.....+xr+.....)
= Coefficient of xr in (1−x)35(1−x)−1
= Coefficient of xr in (1−x)34
=(−1)r.34Cr
Required maximum value is .24C17.
c. .31Cr−5+5×.31Cr−4+10×.31Cr−3+10×.31Cr−2+5×.31Cr−1+.31Cr
=.5C5×.31Cr−5+.5C4×.31Cr−4+.5C3×.31Cr−3+.5C2×.31Cr−2+.5C1×.31Cr−1+.5C0×.31Cr
= Coefficient of xr in (1+x)5(1+x)31
= Coefficient of xr in (1+x)36
=.36Cr
Which has maximum value of .36C18.
d. k∑r=02k−r.(−1)r.37Cr..37−rC37−k
=k∑r=02k−r.(−1)r.37!(37−r)!r!(37−r)!(37−k)!(k−r)!
=37!k!(37−k)!k∑r=02k−r.(−1)r.k!r!(k−r)!
=.37Crk∑r=0.kCr2k−r.(−1)r
=.37Ck(2−1)k
=.37Ck
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Match List-I and List-II.
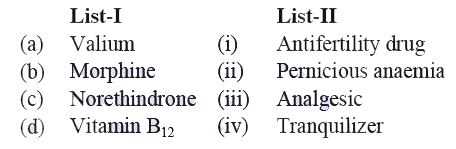 A(a)-(iv),(b)-(iii) , (c) - (ii) , (d)-(i)B(a)-(iv), (b)-(iii),(c)-(i), (d)-(ii)C(a)-(ii),(b)-(iv),(c)-(iii),(d)-(i)D(a)-(i),(b)-(iii),(c)-(iv),(d)-(ii)
A(a)-(iv),(b)-(iii) , (c) - (ii) , (d)-(i)B(a)-(iv), (b)-(iii),(c)-(i), (d)-(ii)C(a)-(ii),(b)-(iv),(c)-(iii),(d)-(i)D(a)-(i),(b)-(iii),(c)-(iv),(d)-(ii)Match the List-I and List-II:
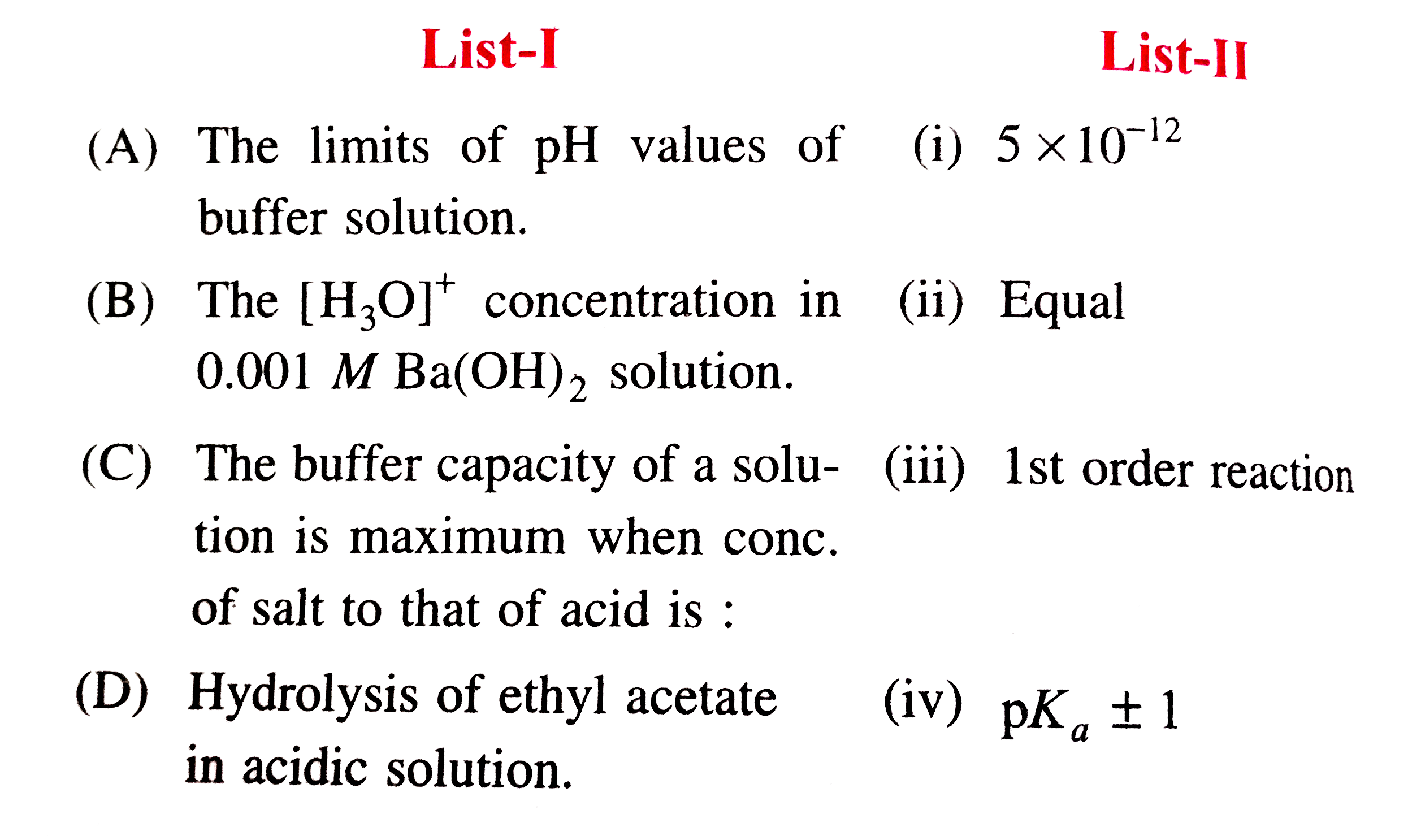 A(A)(B)(C)(D)iviiiiiiB(A)(B)(C)(D)iviiiiiiC(A)(B)(C)(D)iiviiiiiD(A)(B)(C)(D)iviiiiii
A(A)(B)(C)(D)iviiiiiiB(A)(B)(C)(D)iviiiiiiC(A)(B)(C)(D)iiviiiiiD(A)(B)(C)(D)iviiiiiiMatch the List-I and List-II:
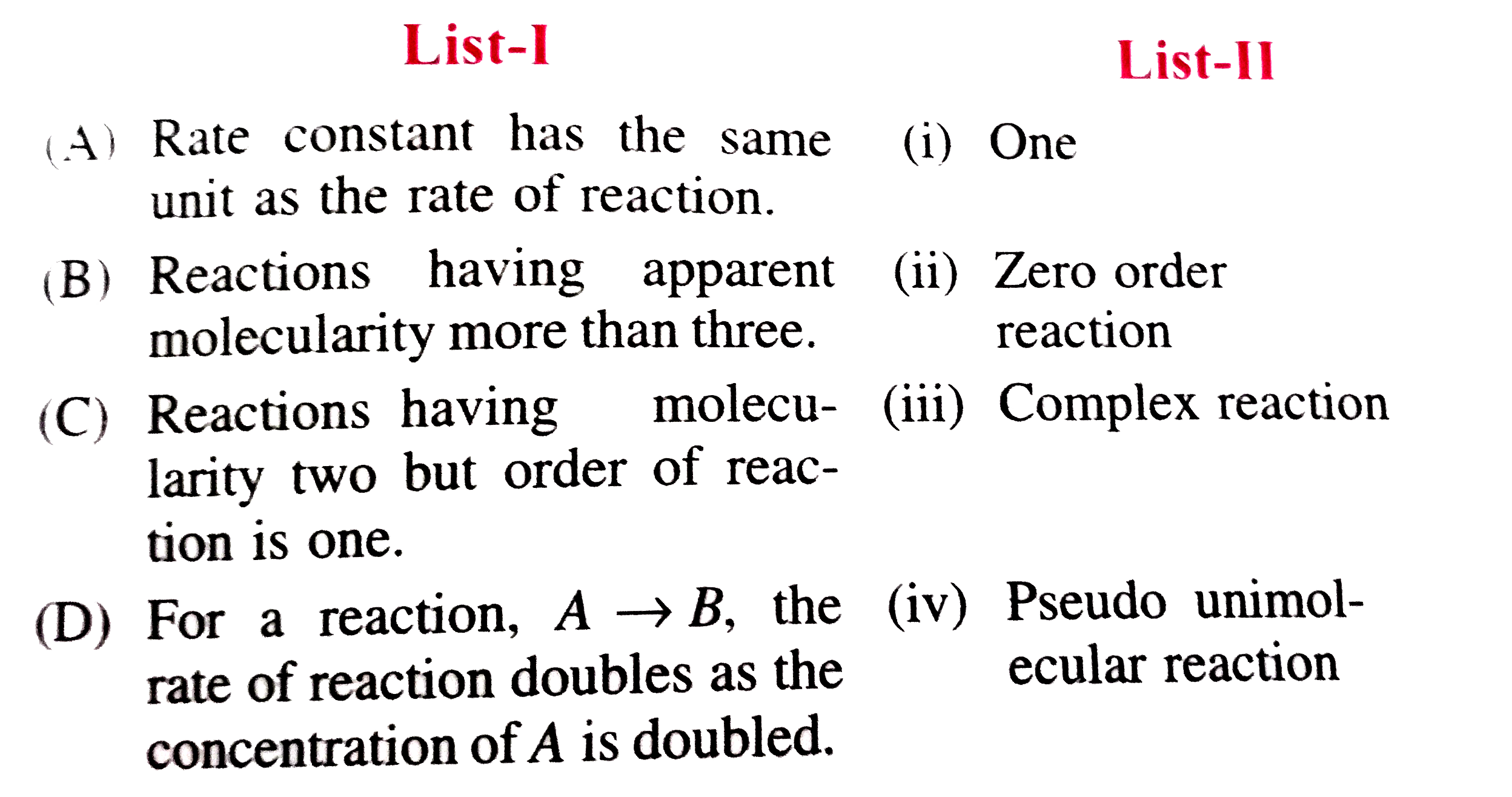 A(A)(B)(C)(D)iiiviiiiB(A)(B)(C)(D)iiiiiiviC(A)(B)(C)(D)iiiiiiviD(A)(B)(C)(D)iiiviiii
A(A)(B)(C)(D)iiiviiiiB(A)(B)(C)(D)iiiiiiviC(A)(B)(C)(D)iiiiiiviD(A)(B)(C)(D)iiiviiii