Marks obtained by four students are : 25, 35, 45, 55.
The average deriations from the mean is
10
9
7
none of these
The correct Answer is:A
To find the average deviation from the mean for the marks obtained by four students (25, 35, 45, 55), we will follow these steps:
Step 1: Calculate the Mean
The mean (average) is calculated by summing all the values and dividing by the number of values.
Mean(xˉ)=25+35+45+554
Calculating the sum:
25+35+45+55=160
Now, divide by the number of students (4):
xˉ=1604=40
Step 2: Calculate the Deviations from the Mean
Next, we calculate the absolute deviations of each mark from the mean:
1. For 25:
|25−40|=|−15|=15
2. For 35:
|35−40|=|−5|=5
3. For 45:
|45−40|=|5|=5
4. For 55:
|55−40|=|15|=15
Step 3: Sum the Absolute Deviations
Now, sum all the absolute deviations calculated in the previous step:
Total Absolute Deviations=15+5+5+15=40
Step 4: Calculate the Average Deviation
Finally, we calculate the average deviation by dividing the total absolute deviations by the number of values (n):
Average Deviation=Total Absolute Deviationsn=404=10
Final Answer
The average deviation from the mean is 10.
---
The mean (average) is calculated by summing all the values and dividing by the number of values.
Next, we calculate the absolute deviations of each mark from the mean:
|25−40|=|−15|=15
|35−40|=|−5|=5
|45−40|=|5|=5
|55−40|=|15|=15
Now, sum all the absolute deviations calculated in the previous step:
Finally, we calculate the average deviation by dividing the total absolute deviations by the number of values (n):
The average deviation from the mean is 10.
Topper's Solved these Questions
- MEASURES OF CENTRAL TENDENCY BOOK - ML KHANNACHAPTER - MEASURES OF CENTRAL TENDENCY EXERCISE - Problem Set (1) (Measures of Disperation)
23 Videos
- MEASURES OF CENTRAL TENDENCY BOOK - ML KHANNACHAPTER - MEASURES OF CENTRAL TENDENCY EXERCISE - SELF ASSESSMENT TEST
5 Videos
- MEASURES OF CENTRAL TENDENCY BOOK - ML KHANNACHAPTER - MEASURES OF CENTRAL TENDENCY EXERCISE - ASSERTION / REASON
1 Videos
- MAXIMA AND MINIMA BOOK - ML KHANNACHAPTER - MAXIMA AND MINIMA EXERCISE - MISCELANEOUS EXERCISE (COMPREHENSION)
3 Videos
- NUMERICAL METHODSBOOK - ML KHANNACHAPTER - NUMERICAL METHODSEXERCISE - SELF ASSESSMENT TEST
10 Videos
Similar Questions
The average marks of 39 students of a class is 50. The marks obtained by 40th student are 39 more than the average marks of all the 40 student are 39 more than the average marks of all the 40 students. Find the mean marks of all the 40 students.
View SolutionThe average marks of 39 students of a class is 50. The marks obtained by 40th student are 39 more than the average marks of all the 40 student are 39 more than the average marks of all the 40 students. Find the mean marks of all the 40 students.
View Solution
Knowledge Check
The average marks obtained by a class of 60 students is 65. The average marks of half of the students is found to be 85. The average marks of the remaining students is
A35B45C55D65The average marks obtained by 240 students in a certain examination is 35. If the average marks of the passed candidates are 39 and that of the failed candidates are 15, then the total number of candidates who passed the examination is:
A225B180C200D210Marks obtained by 7 students in a subject are 30, 55, 75, 90, 50, 60, 39. The number of students securing marks less than the mean marks is
A7B6C5D4
The table given below shows the marks obtained by 6 students in 3 subjects.
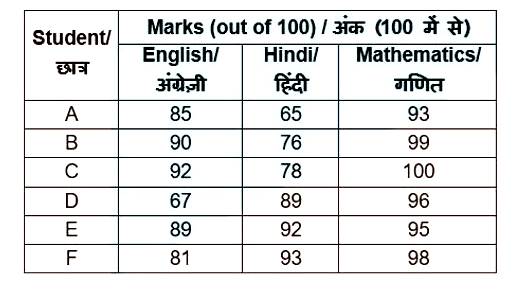
What are the average marks per students in Mathematics?
View SolutionIn a class of 15 students, the total marks obtained by all the students in a test is 600. Find the average mark of the class.
View SolutionThe average marks obtained by the students in a class are 43. If the average marks obtained by 25 boys are 40 and the average marks obtained by the girl students are 48, then what is the number of girl students in the class?
View SolutionThe average marks obtained by the students in a class are 43. If the average marks obtained by 25 boys are 40 and the average marks obtained by the girl students are 48, then what is the number of girl students in the class?
(a)15
(b)17
(c)18
(d)20
View SolutionThe average marks obtained by 120 students in an examination is 30. If the average marks of passed students is 40 and that of the failed students is 10, what is the 25% of the number of students who passed the examination?
View Solution
