Match the conic in List I with the statements/expressions in List II.

Text Solution
The correct Answer is:d→q,s
If |z−z1|−|z−z2|=k where k<|z1−z2|, then locus of variable point 'z' on branch of the hyperbola with fixed points z1 and z2
Clearly distance between complex numbers '2' and '−2' is 4 which is less then 3.
So, locus of z is a branch of the hyperbola.
s. If eccentricity is [1,∞), then the conic can be a parabola (if e = 1) and a hyperbola if e∈(1,∞).
Note. Solutions of the remaining parts are given in their respective chapters.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Match the List-I with List-II:
 A(I)(II)(III)(IV)1245B(I)(II)(III)(IV)5436C(I)(II)(III)(IV)2611D(I)(II)(III)(IV)6251
A(I)(II)(III)(IV)1245B(I)(II)(III)(IV)5436C(I)(II)(III)(IV)2611D(I)(II)(III)(IV)6251
Match the statements given in List I with the values given in List II.

View SolutionMatch the List -I with List - II.
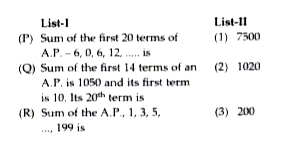
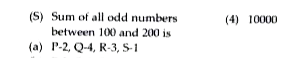
View SolutionMatch the statements in List I with the correct answer from List II.

View SolutionMatch the List-I with List-II :

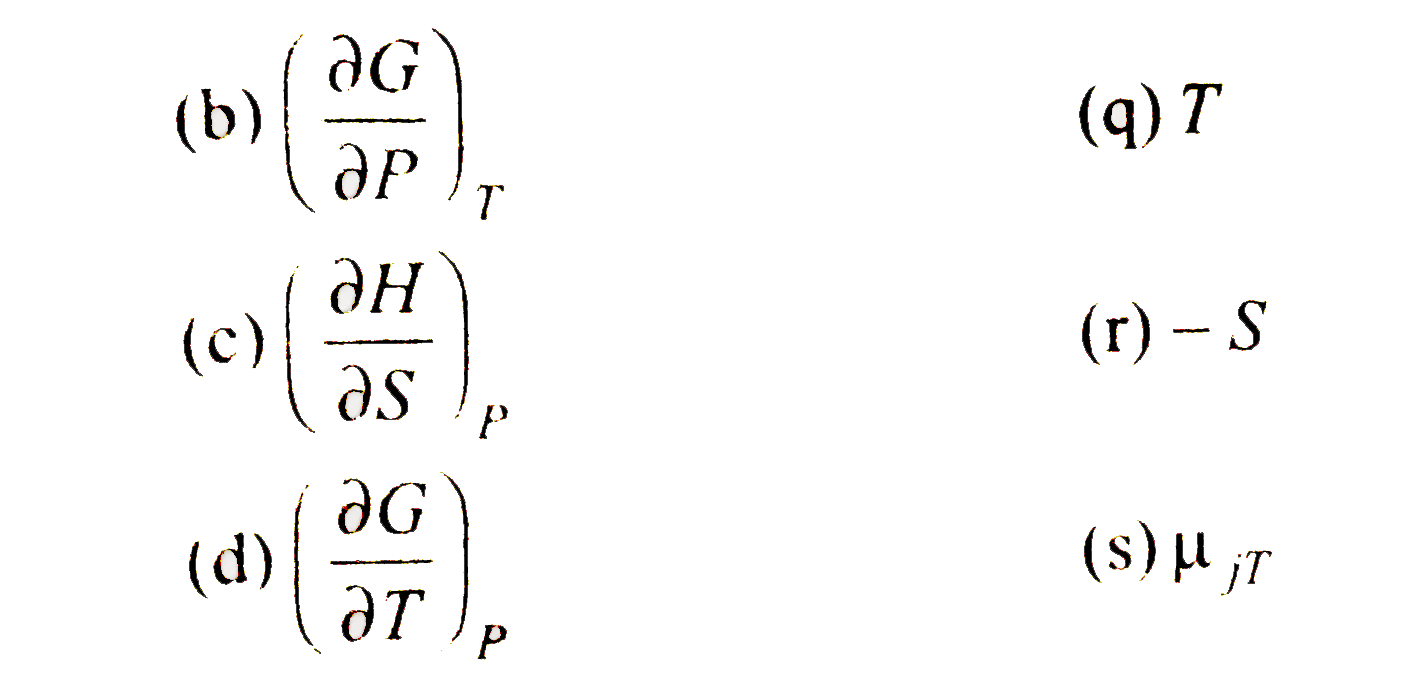
View SolutionMatch the list I with list II :
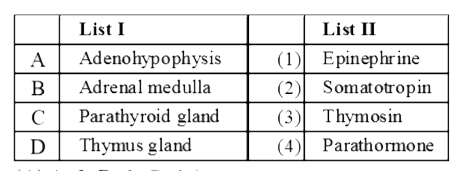
View SolutionMatch List I with List II

View SolutionMatch List I with List II

View Solution



