Match the statements/expressions in List I statements/expression in List II

Text Solution
The correct Answer is:a→p,r,s;b→p

Given 2(a2−b2)=c2
⇒2(sin2X−sin2Y)=sin2Z
⇒2sin(X+Y)sin(X−Y)=sin2Z
⇒2sin(π−Z)sin(X−Y)=sin2Z
⇒sin(X−Y)=sinZ2...(i)
∴λ=sin(X−Y)sinZ=12
Now cos(nπλ)=0
⇒cos(nπ2)=0
∴n=1,3,5

1+cos2X−2cos2Y=2sinXsinY
2cos2X−2cos2Y=2sinXsinY
1−sin2X−1+2sin2Y=sinXsinY
sin2X+sinXsinY=2sin2Y
sinX(sinX+sinY)=2sin2Y
⇒a(a+b)=2b2
⇒a2+ab−2b2=0
⇒(ab)2+ab−2=0
⇒ab=−2,1
⇒ab=1
Note : Solutions of the remaining parts are given in their respecitive chapters.
|
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - JEE Main Previous Year
2 Videos
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBOOK - CENGAGECHAPTER - PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEEXERCISE - Question Bank
32 Videos
Similar Questions
Knowledge Check
Match the statements/expressions given in List I with the values given in List II.
 AabcdsrqpBabcdqsrpCabcdsrpqDabcdqspr
AabcdsrqpBabcdqsrpCabcdsrpqDabcdqspr
Match the conic in List I with the statements/expressions in List II.

View SolutionMatch the statements given in List I with the values given in List II.

View SolutionLet f(x)=x2−6x+5x2−5x+6. Then match the expressions/statements in List I with expression /statements in List II.

View SolutionLet f(x)=x2−6x+5x2−5x+6. Then match the expressions/statements in List I with expression /statements in List II.

View SolutionMatch the statements in List I the appropriate answer in List II.

View SolutionMatch the statements given in the List-I with the equations given in List-II.
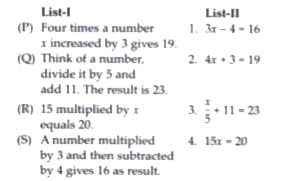
View SolutionMatch the statements in List I with the correct answer from List II.

View Solution



