Match the following lists and then choose the correct code.

A
r,s,p,q
B
s,p,r,q
C
q,s,p,r
D
p,r,s,q
Video Solution
Text Solution
The correct Answer is:3
a. Let the length of the common chord be 2a. Then,
√9−a2+√16−a2=5
or √16−a2=5−√9−a2
or 16−a2=25+9−a2−10√9−a2
or 10√9−a2=18
or 100(9−a2)=324
i.e., 100a2=576
or a=√576100=2410
∴2a=245=k5or =24
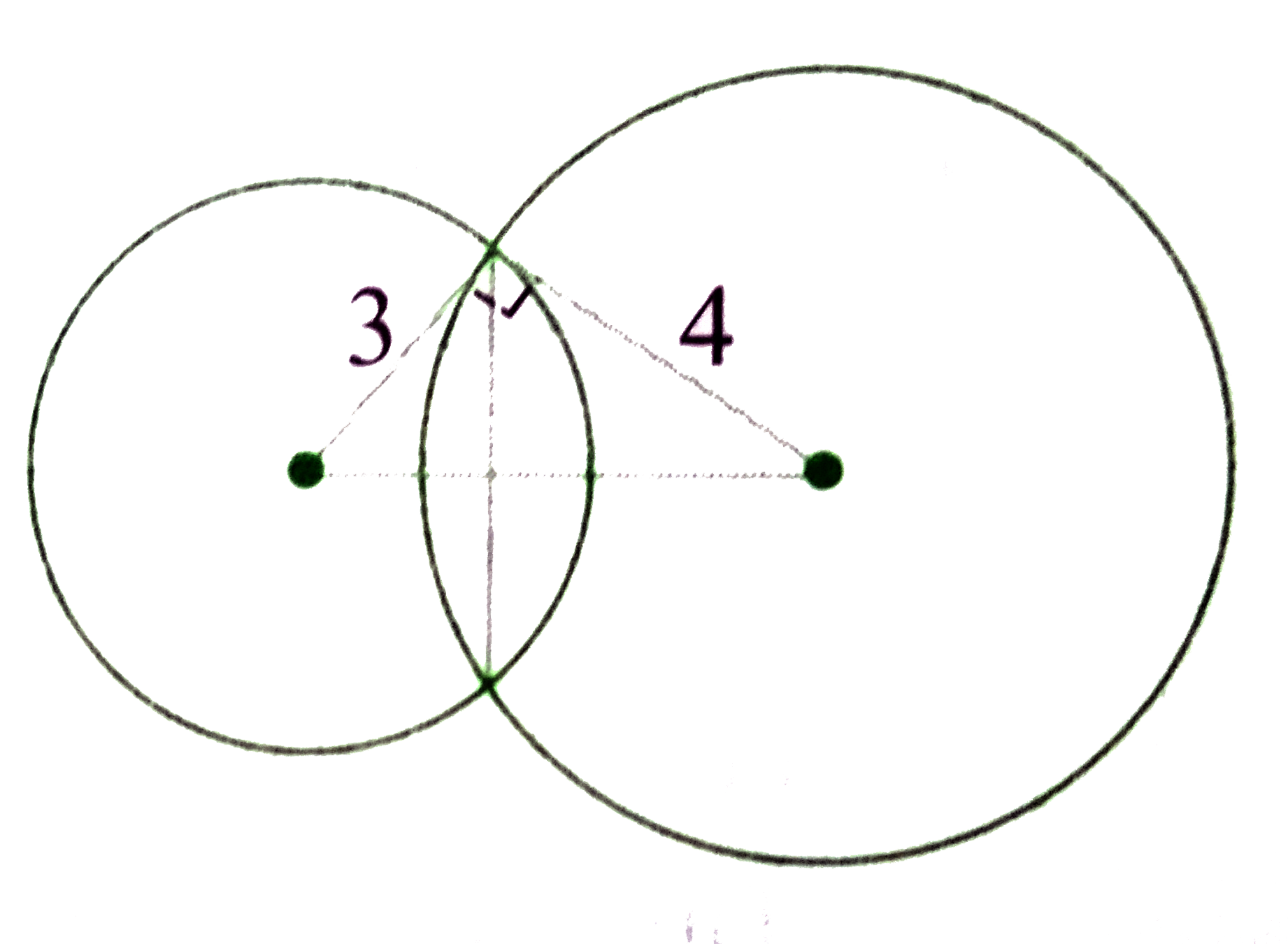
b. The equation of common chord is 6x+4y+p+q=0.
The common chord passes through the center (−2,−6) of the circle x2+y2+4x+12y+p=0 . Therefore,
p+q=36
c. The equation of the circle is 2x2+2y2−2√2x−y=0
Let (α,0) be the midpoint of a chord . Then the equation of the chord is
2αx−√2(x+α)−12(y+0)=2α2−2√2α
Since it passes through the point (√2,1/2) , we have
2√2α−√2(√2+α)−14=2α2−2√2α
i.e., 8α2−12√2α+9=0
i.e., (2√2α−3)2=0
i.e., α=32√2
Therefore, the number of chords is 1.
d. Midpoint of AB ≡(1,4).
The equation perpendicular bisector of AB is x=1
A diameter of the circle is 4y=x+7
Therefore, the center of the circle is (1,2)
Hence, the sides of the rectangle are 8 and 4. Therefore, area =32
|
Topper's Solved these Questions
Similar Questions
Match the following and choose the correct option

View SolutionMatch the following lists:
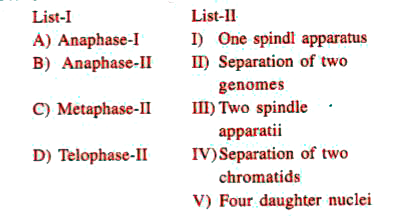
The correct match is
View SolutionStudy the following list and find out the correct match

View SolutionStudy the following lists and find the correct match
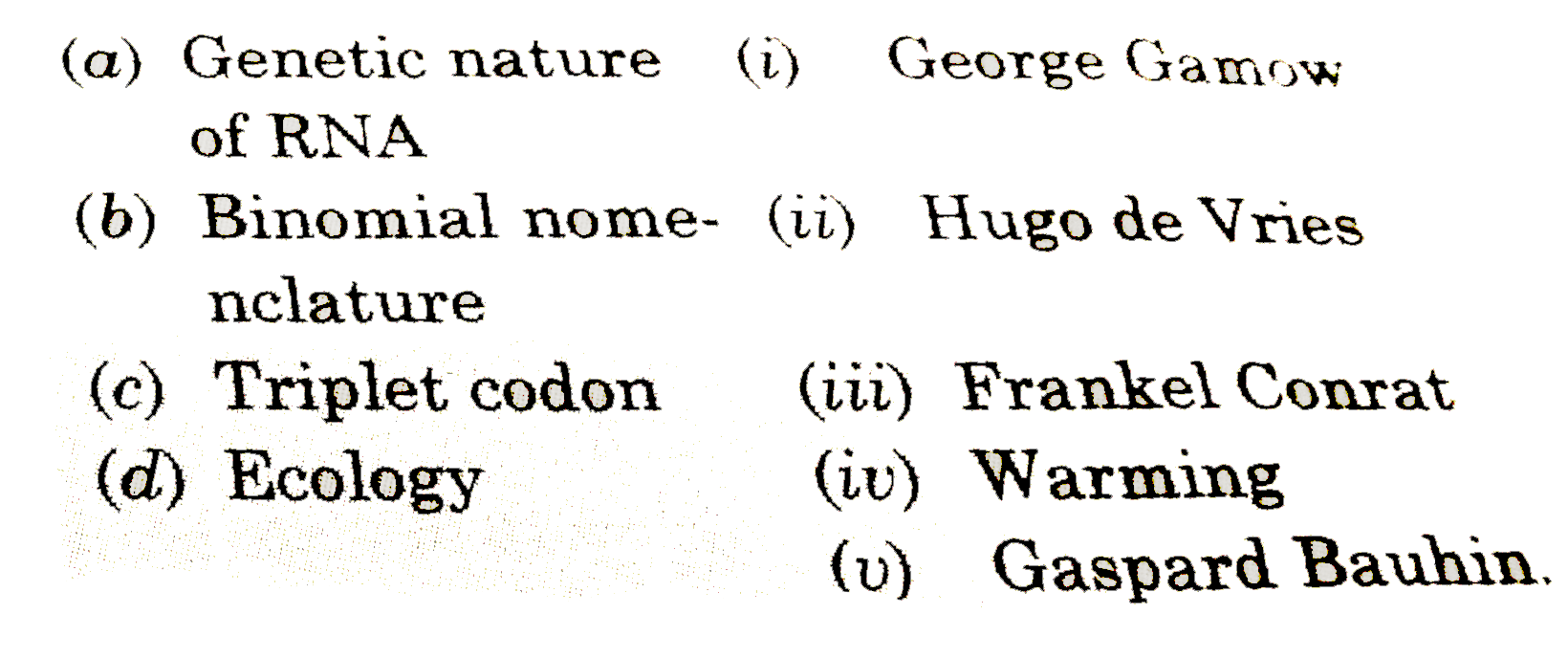
View SolutionStudy the following lists and find the correct match
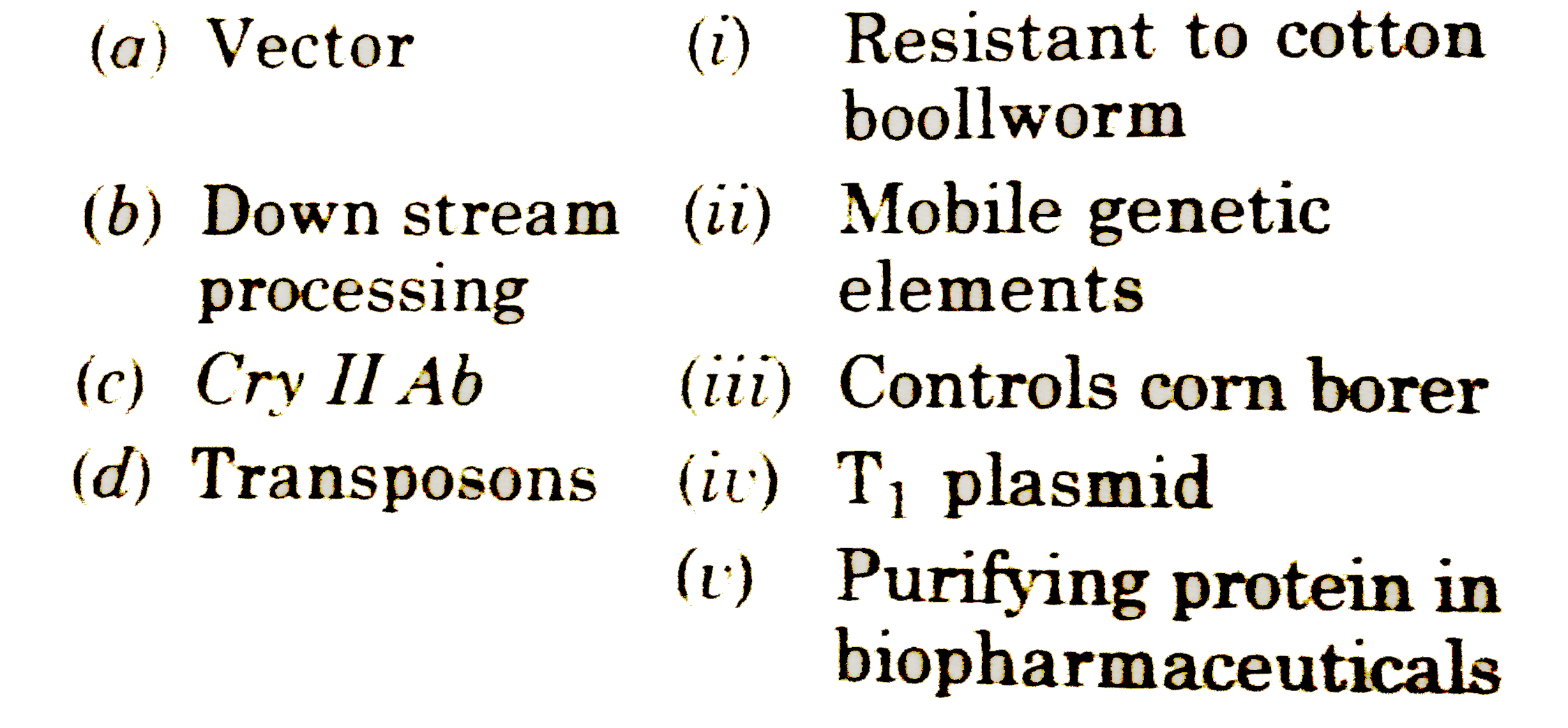
View SolutionMatch list I with list II and choose the correct answer from the codes given below :

View SolutionMatch the List with List II and choose the correct option from the codes given below:

View SolutionMatch list I with list II and then select the correct answer from the codes given below
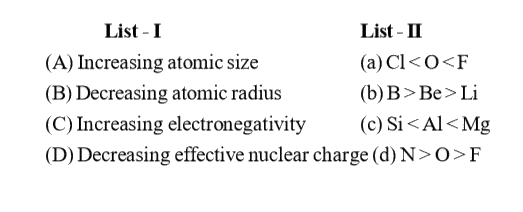
Codes :
View SolutionMatch List I with List II and choose the correct answer
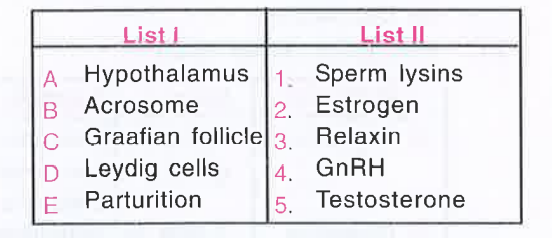
View SolutionStudy the following lists:

The correct match is
View Solution
