Maximise Z=x+y subject to x+4y≤8,2x+3y≤12,3x+y≤9,x≥0,andy≥0
Text Solution
The correct Answer is:N/a
Here the given LPP is
Maximise Z=X+Y subject to
x+4y≥8,2x+3y≤12,3x+y≤9,x≥0,y≥0
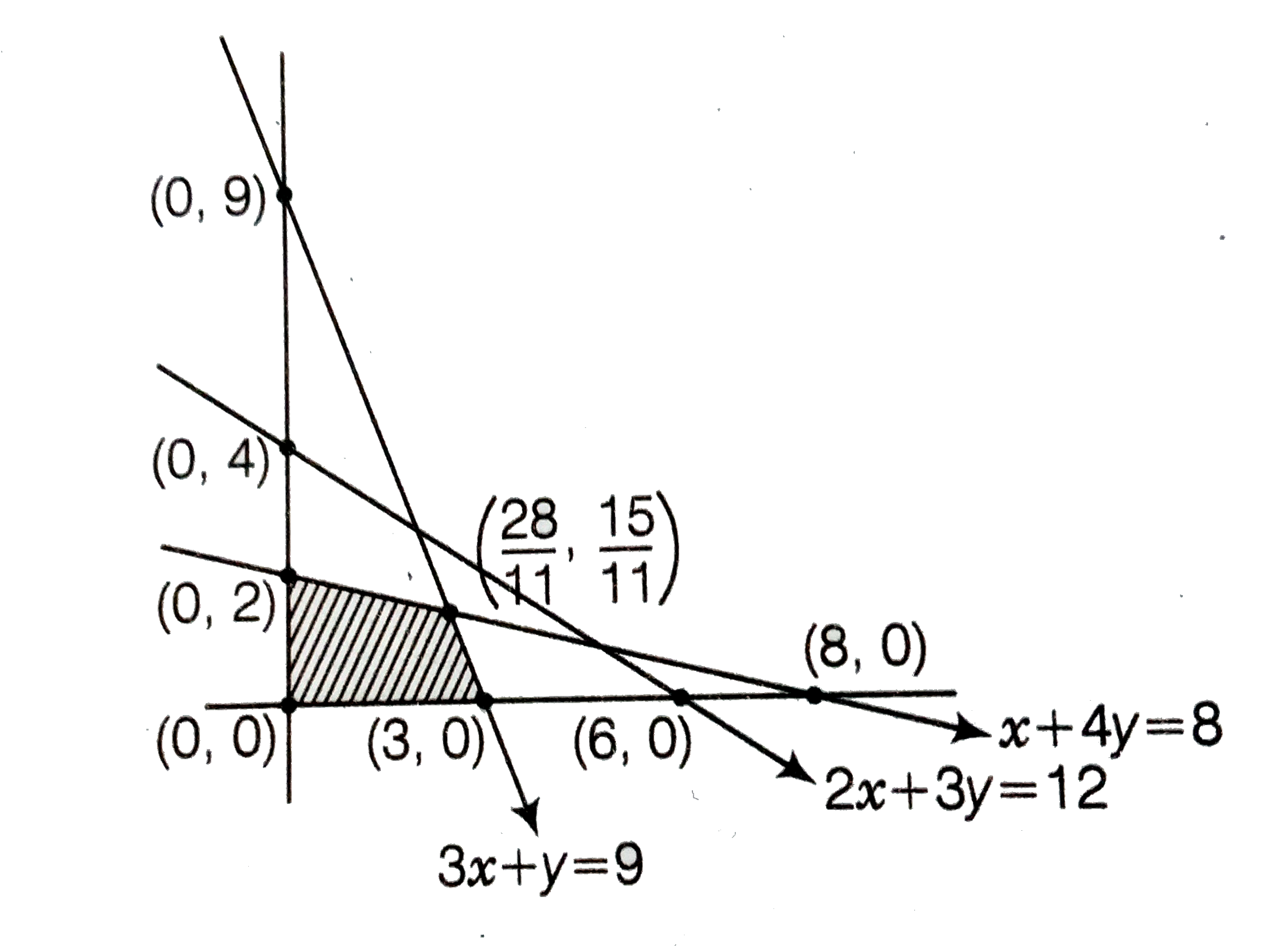
On solving x+4y=8 and 3x+y=9 we get
x=2811,y=1511
From the feasible region, it is clear that coordinates of corner points are (0,0), (3,0) 2811,1511 and (0,2)
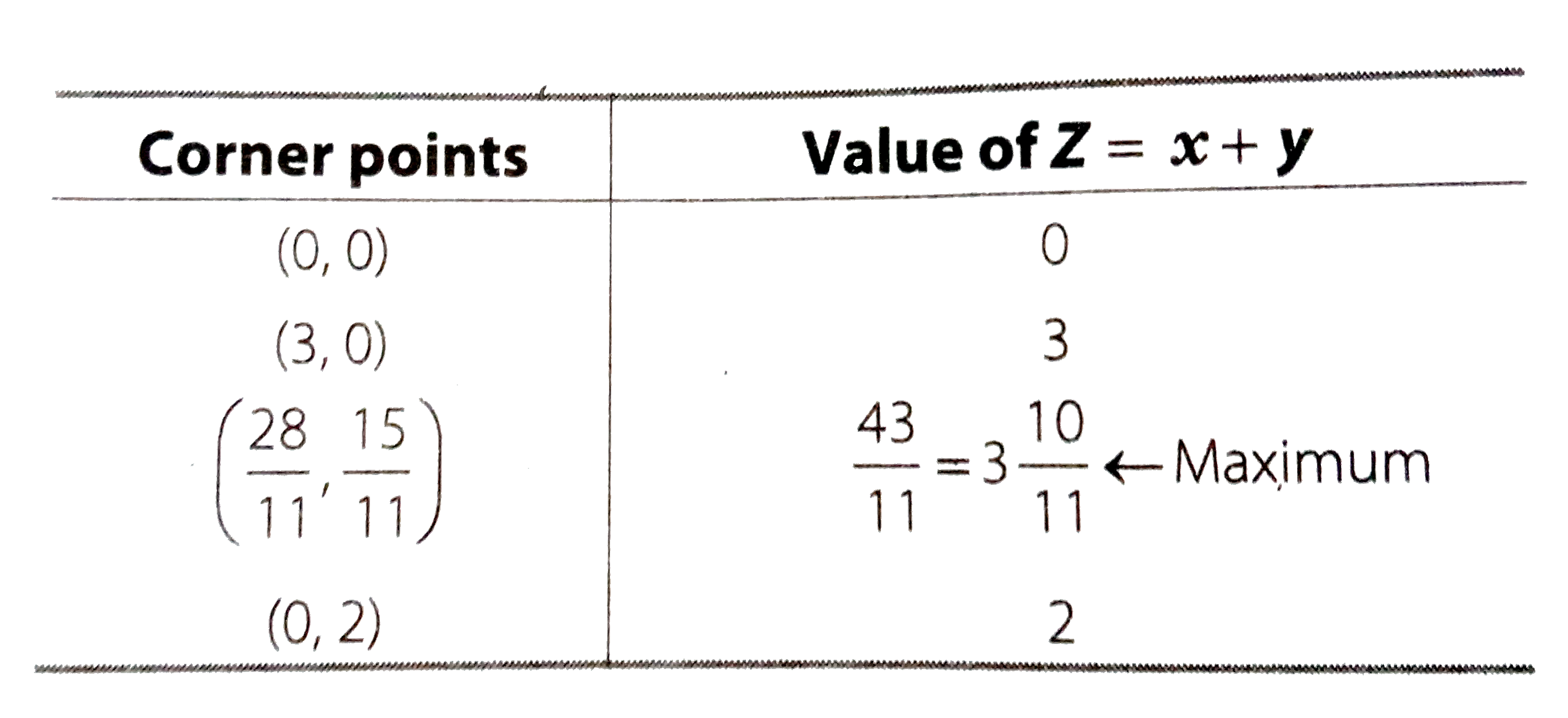
Hence, the maximum value is 31011
|
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - OBJECTIVE
8 Videos
- LINEAR PROGRAMMINGBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - FILLERS
7 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Fillers
18 Videos
- MATRICESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MATRICESEXERCISE - Solved example
101 Videos
Similar Questions
x+y≤10,4x+3y≤24,x≥0,y≥0
View SolutionMaximize :
z=3x+5y
Subject to : x+4y≤24
3x+y≤21
x+y≤9
x≥0,y≥0
View SolutionMinimise Z=−3x+4y
subject to x+2y≤8,3x+2y≤12,x≥0,y≥0.
View SolutionMaximise Z=x+y, subject to x−y≤−1,−x+y≤0,x,y≥0.
View SolutionMinimize Z=3x+2y subject to x+y≤8,x,y≥0.
View SolutionMaximise Z=5x+3y
subject to3x+5y≤15,5x+2y≤10,x≥0,y≥0.
View SolutionMaximize z=4x+5y, subject to
2x+y≥7,2x+3y≤15,x≤3,x≥0,y≥0
View Solutionx−2y≤2,x+y≤3,−2x+y≤4,x≥0,y≥0
View SolutionZ=4x+y
x+y≤50,3x+y≤90,x≥0,y≥0
View SolutionMinimize z=6x+2y, subject to 5x+9y≤90,x+y≥4,y≤8,x≥0,y≥0.
View Solution
