Maximize z=6x+4y subject to constraints,
$x \leq 2, x + y \leq 3, - 2 x + y \leq 1, x y \geq 0$
Also find the maximum value of 'z'.

Video Solution

Text Solution

Verified by Experts

Consider x+y=3 " " -2x+y=1

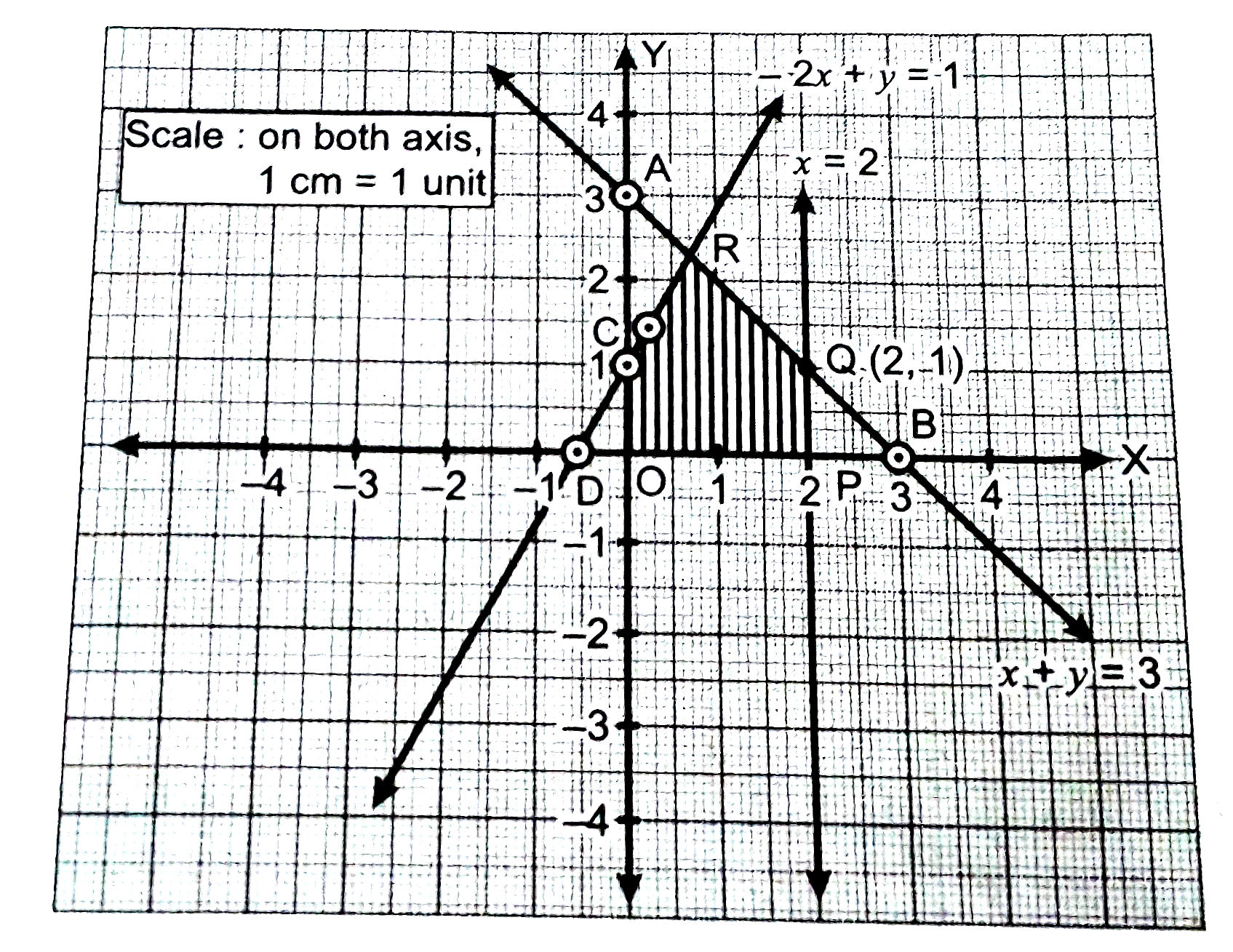
Shaded region OPQRC is the feasible region with vertices $O (0, 0), P (2, 0), Q, R and C (0, 1) . Q$ is a point of intersection of lines x=2 and x+y=3. Solving these equations, we get Q=(2,1) . R is the point of intersection of lines x+y=3 and -2x+y=1.
$x + y = 3 ... ... (i)$
$- 2 x + y = 1 ... ... (i i)$
$\frac{+ - -}{3 x = 2}$
$∴ x = \frac{2}{3}$
Substituting $x = \frac{2}{3}$ in equation (i)
$\frac{2}{3} + y = 3$
$∴ y = 3 - \frac{2}{3} = \frac{9 - 2}{3} = \frac{7}{3}$
$∴ R = (\frac{2}{3}, \frac{7}{3})$ .
Now $z = 6 x + 4 y$
$∴ z (0, 0) = 6 \times 0 + 4 \times 0 = 0$
$z (2, 0) = 6 \times 2 + 0 = 12$
$z (2, 1) = 6 \times 2 + 4 \times 1 = 16$
$z (\frac{2}{3}, \frac{7}{3}) = 6 \times \frac{2}{3} + 4 \times \frac{7}{3}$
$= 4 + \frac{28}{3} = \frac{40}{3} = 13.33$
$z (0, 1) = 6 \times 0 + 4 \times 1 = 4$
$∴$ z has maximum value at (2,1)
$∴$ Maximum value of z is 16 at x=2 and y=1.

Updated on:21/07/2023