Nazinia is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that h
Description of the figure :
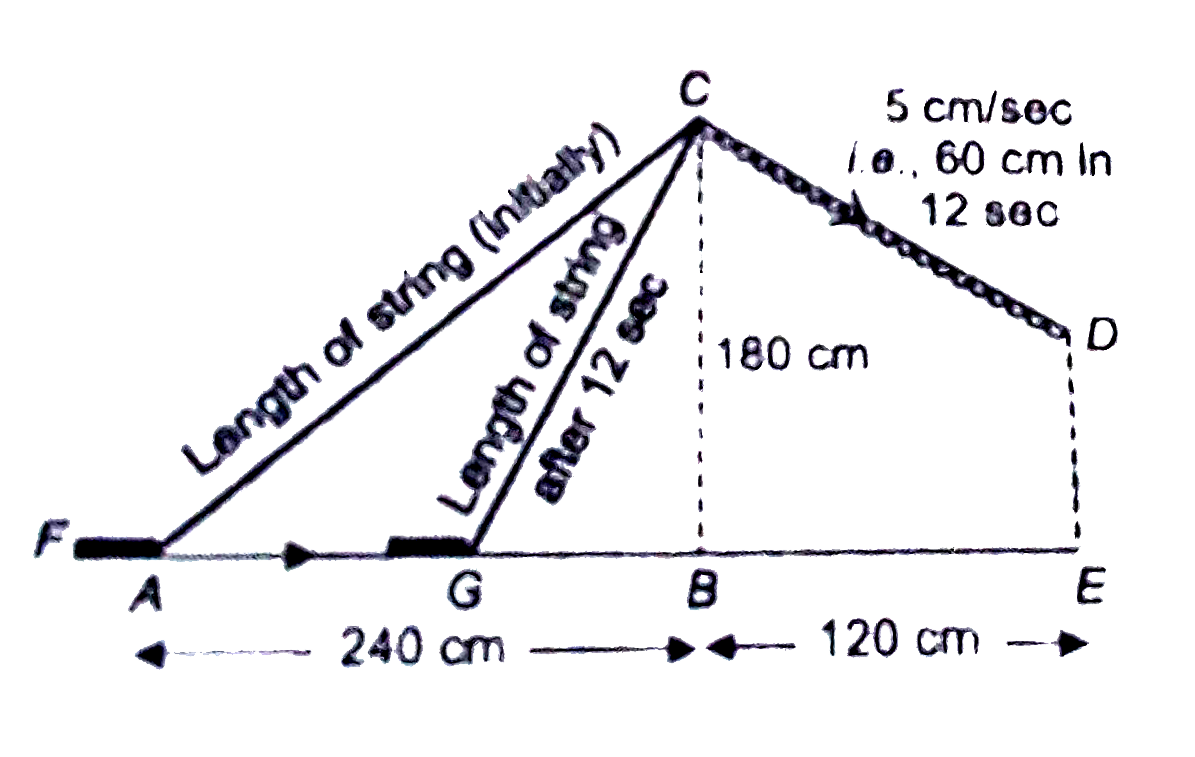
C→ Tip of fishing rod DC
AC→ stiring , AF→ fly
Intially string was AC = √(180)2+(240)2
( by pythagores theorem)
⇒ AC=√32400+57600
= 300 cm
BUT
When Nazima pulls in the string at the rate of 5cm/sec, she will pull 5×12cm in 12 sec. you can imagine that string will pull out 60 cm from C towards D. Now remaining string CA will become CG = 300-60=240 cm , because when string will pull in , its end point A as will as fly will move from A towards G. So, horizontal distance of fly at G ( now) from Nazima at E will be EG.
Now, GB2=CG2−CB2 ( by pythagoras theorem)
=(240)2−(280)2=57600−32400=25200
GB=√25200=10√252=60√7
=60×2.64575=158.745cm
Reqyuired distance = EG = GB + BE= 158.745 + 120
= 278.745 cm = 2.79 m ( approx).
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar14videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6a23videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions5videos
STATISTICS
- BOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions5videos
VOLUME AND SURFACE AREA OF SOLIDS
Similar Questions
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod.
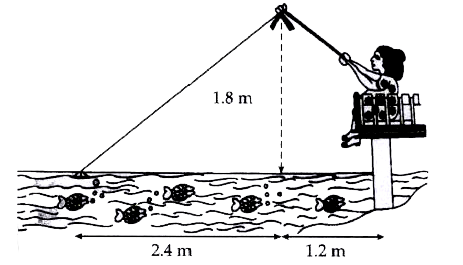
Assuming that her string (form the tip of her rod to the fly) is taut, how much string does she have out (see figure)?View SolutionNazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A bird is flying 3m above the surface of water. To a fish underwater, the height of the bird from the water surface appears to be
A2.25mB3.33mC4mD4/3m - Question 2 - Select One
An L-shaped tube with a small orifice is held in a water stream as shown in fig. The upper end of the tube is 10.6 cm above the surface of water. What will be the height of the jet of water coming from the orifice? Velocity of water stream is 2.45m/s
 AZeroB20.0cmC10.6cmD40.0cm
AZeroB20.0cmC10.6cmD40.0cm - Question 3 - Select One
An L-shaped tube with a small orifice is held in a water stream as shown in fig. The upper end of the tube is 10.6cm above the surface of water. What will be the height of the jet of water coming from the orifice? (Velocity water steam is 2.45m/s)
 AZeroB20.8cmC10.6cmD40.0cm
AZeroB20.8cmC10.6cmD40.0cm
Find the capacity of water tank, in litres, whose dimensions are 4.2 m, 3 m and 1.8 m?
View SolutionIn a pond of water, a flame is held 2 m above the surface of the water. A fish is at depth of 4 m from the water surface. Refractive index of water is 43. The apparent height of the flame from the eyes of fish is -
View SolutionA bird is flying 3m above the surface of water,If the bird is diving vertically down with speed =6m/shis apparent velocity as seen by a stationary fish underwater is:
View SolutionA fish lies at the bottom of a 4m deep water lake. A bird flies 6m above the water surface and refractive index of water is 4/3 . Then the distance between
View SolutionA man looks down on a fish of length 20 cm. His eye is 2m above the surface of the water (μ=4/3) and the fish is 2m below the surface as shown in the figure the ratio of angular width Δθ of the fish as seen by the man in presence of water to the Δθ in the absence of water is (Δθ is small)
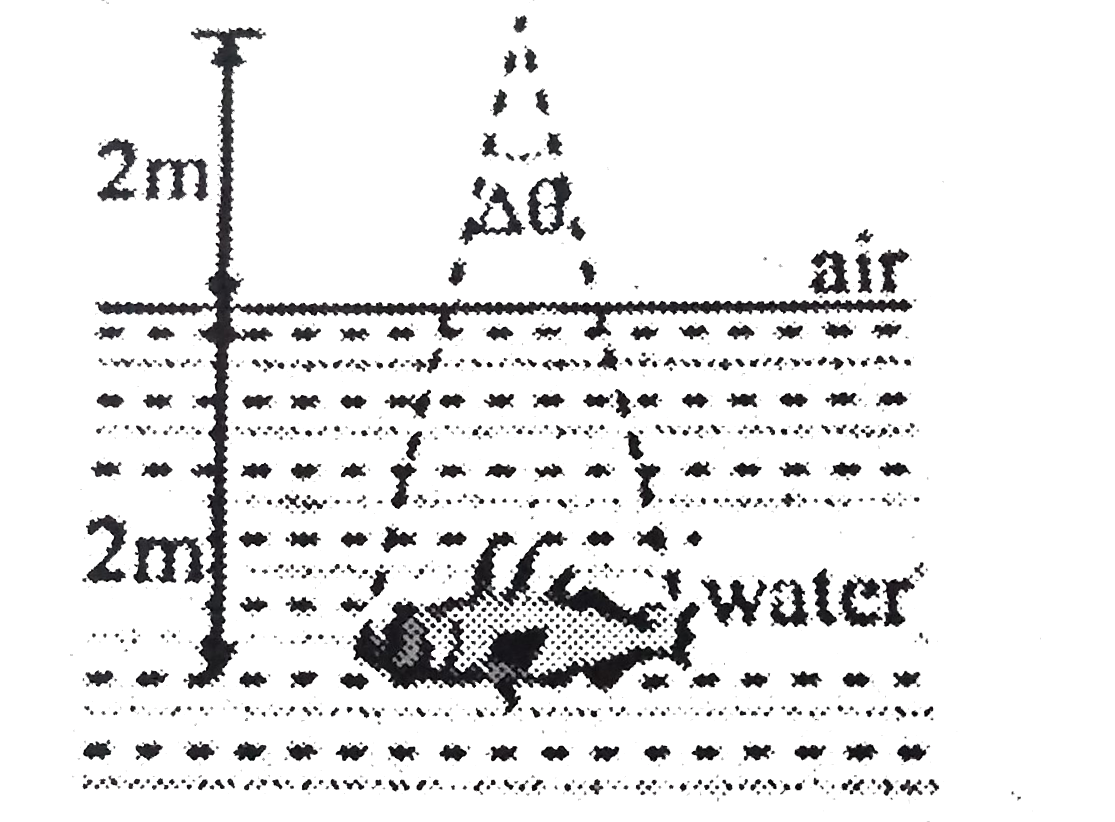 View Solution
View Solution

