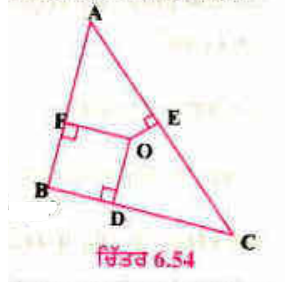
O' is any point in the interior of a triangle ABC. OD⊥BC, OE⊥AC and OF⊥AB, Show that
OA2+OB2+OC2˜nOD2˜nOF2=AF2+BD2+CE2
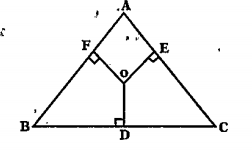 Solution in Telugu
Solution in Telugu
Step by step video & image solution for O' is any point in the interior of a triangle ABC. OD bot BC, OE bot AC and OF bot AB, Show that OA^2 + OB^2 + OC^2 overset(~)n OD^2 overset(~)n OF^2 = AF^2 + BD^2 + CE^2 by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
‘O’ is any point in the interior of a triangle ABC. If OD⊥BC,OE⊥AC and OF ⊥ AB, show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BE2.
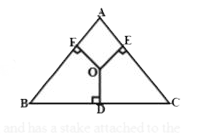
View Solution‘O’ is any point in the interior of a triangle ABC. If OD⊥BC,OE⊥AC and OF ⊥ AB, show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BE2.
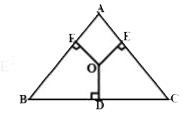
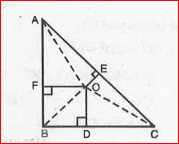
View SolutionIn the figure given below, O is point in the interior of a triangle ABC, OD⊥BC, OE⊥AC and OF⊥AB. Show that
(i) OA2+OB2+OC2+OD2−OE2−OF2=AR2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BF2
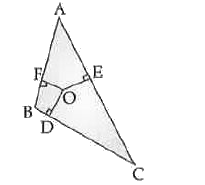
View SolutionIn the given figure, O is a point in the interior of a DeltaABC, OD⊥BC,OE⊥AC and OF⊥AB. Show that :
OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2.
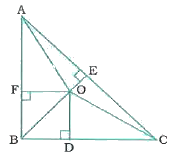
View SolutionIn the given figure, O is a point in the interior of a DeltaABC, OD⊥BC,OE⊥AC and OF⊥AB. Show that :
AF2+BD2+CE2=AE2+CD2+BF2.
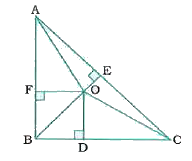
View SolutionIn fig., O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that:- OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2 .
View SolutionIn fig., O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that:- AF2+BD2+CE2=AE2+CD2+BF2 .
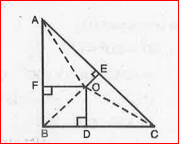
 .
.
View Solutionਚਿੱਤਰ 6.54 ਵਿੱਚ, ΔABC ਦੇ ਵਿਚ ਸਥਿਤ ਕੋਈ ਬਿੰਦੂ O ਹੈ ਅਤੇ OD⊥BC,OE⊥AC ਅਤੇ OF⊥ABਹੈ।ਦਿਖਾਓ ਕਿ OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
View Solution
