O is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E, find the length AB.

Video Solution

Text Solution

Verified by Experts

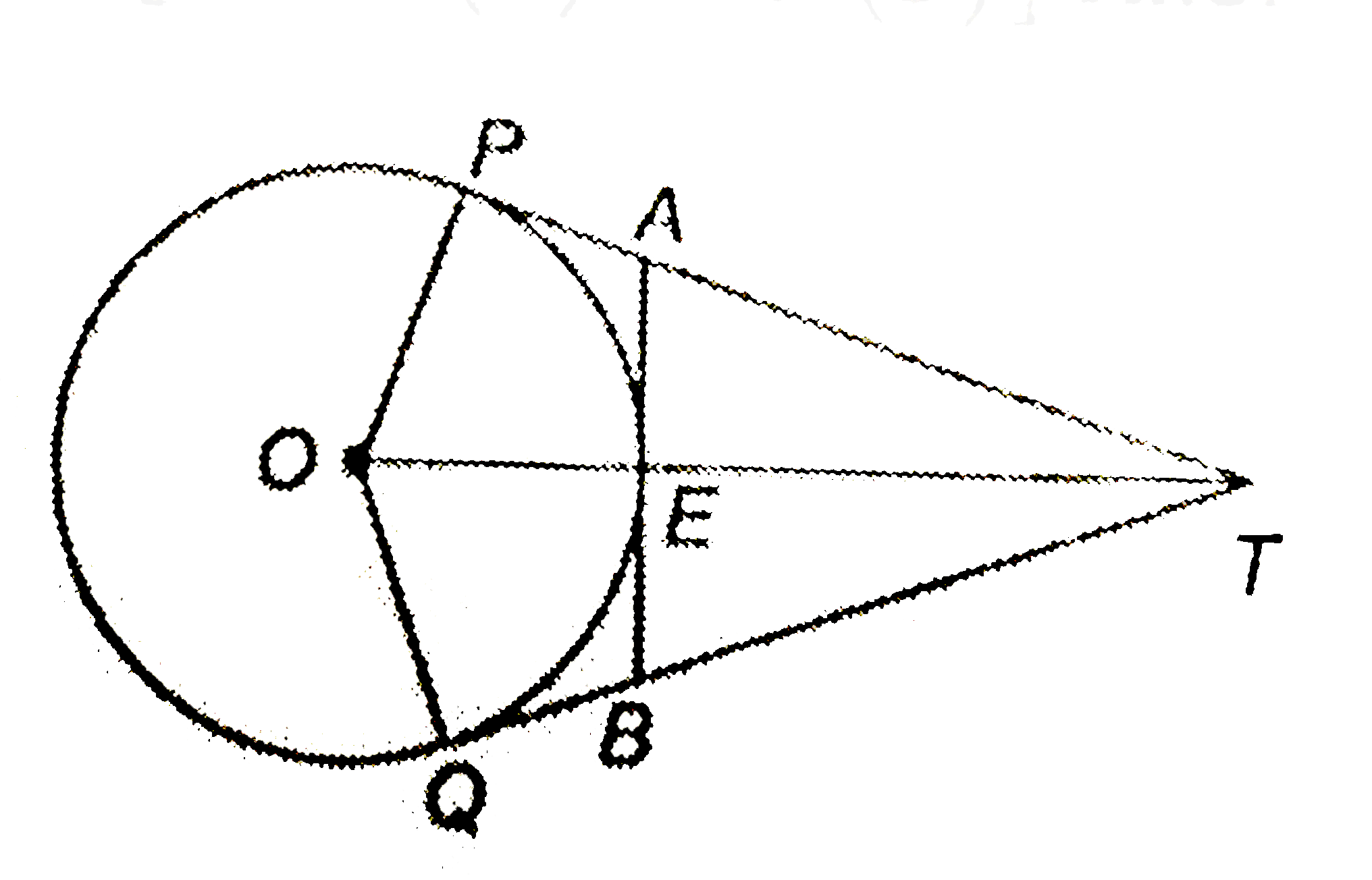
Since, $∠ O P T = 90^{\circ}$
(radius through point of contact is $⊥$ to the tangent)
$∴$ In right $△ O P T,$
$O P^{2} + P T^{2} = O T^{2}$ (by Pythagoras theorem)
$\Rightarrow P T^{2} = O T^{2} - O P^{2}$
$\Rightarrow P T^{2} = {(13)}^{2} - {(5)}^{2} = {(12)}^{2}$
$\Rightarrow P T = 12 c m$
Let $A P = x c m$
$∴ A E = A P = x$ (lengths of tangents from an external point are equal)
$∴ A T = T P - A P = 12 - x$
$E T = O T - O E = 13 - 5 = 8 c m$
Now, since $∠ A E O = 90^{\circ}$ (radius through point of contact is $⊥$ to the tangent)
$∴ ∠ A E T = 90^{\circ}$ (L.P.A)
$∴$ In right $△ A E T,$ by Pythagoras theorem,
$A E^{2} + E T^{2} = A T^{2}$
Circles
$\Rightarrow x^{2} + {(8)}^{2} = {(12 - x)}^{2}$
$\Rightarrow x^{2} + 64 = 144 + x^{2} - 24 x$
$\Rightarrow 24 x = 144 - 64 = 80$
$\Rightarrow x = \frac{80}{24} = \frac{10}{3}$
Similarly, $B E = \frac{10}{3} c m$
$∴ A B = A E + B E = (\frac{10}{3} + \frac{10}{3}) c m = \frac{20}{3} c m$
Hence, $A B = \frac{20}{3} c m$

Updated on:21/07/2023

Type V: O is the center of the circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E . If AB is the tangent to the circle at E; find the length of AB.
A $\frac{10}{3}$
B $\frac{20}{3}$
C $\frac{16}{3}$
DCannot be determined
$O$ is the centre of a circle of radius $5 c m .$ $T$ is a point such that $O T = 13 c m a n d O T$ intersects the circle at $E .$ If $A B$ is the tangent to the circle at $E,$ find length of $A B .$
A20 cm
B $\frac{20}{3} c m$
C $10 c m$
D25 cm
Tangents PT and QT are drawn on a circle of radius 5 cm from point T which is 13 cm away from the circle. What is the length (in cm) of AB?
A $\frac{10}{3} c m$
B $\frac{20}{3} c m$
C $\frac{40}{3} c m$
D $\frac{16}{3} c m$