O is the centre of a circle with radius 5 cm. LM is the diameter of the circle. P is a point on the plane of the circle such that LP = 6 cm and MP = 8 cm. Then P lies.
on LM
outside the circle
inside the circle
on the circle
The correct Answer is:D
To solve the problem step by step, we will analyze the given information and apply the Pythagorean theorem.
1. Identify the Circle's Properties:
- The center of the circle is O.
- The radius of the circle is 5 cm.
- Therefore, the diameter LM is twice the radius:
LM=2×5 cm=10 cm
2. Position the Points:
- Let L and M be the endpoints of the diameter, with O being the midpoint.
- We can place L at (-5, 0) and M at (5, 0) on a coordinate plane for simplicity. Thus, O is at (0, 0).
3. Locate Point P:
- We know that:
- LP=6 cm
- MP=8 cm
4. Apply the Pythagorean Theorem:
- According to the Pythagorean theorem, in triangle LPM:
LP2+MP2=LM2
- Substitute the known lengths:
62+82=LM2
- Calculate the squares:
36+64=LM2
100=LM2
- Since we have already calculated LM=10 cm, we confirm:
LM2=102=100
5. Determine the Type of Triangle:
- Since LP2+MP2=LM2, triangle LPM is a right triangle with the right angle at point P.
6. Conclusion:
- According to the properties of circles, if a triangle is inscribed in a circle and one of its angles is a right angle, then the vertex of the right angle lies on the circumference of the circle.
- Therefore, point P lies on the circumference of the circle.
Final Answer:
Point P lies on the circumference of the circle.
---
- The center of the circle is O.
- The radius of the circle is 5 cm.
- Therefore, the diameter LM is twice the radius:
LM=2×5 cm=10 cm
- Let L and M be the endpoints of the diameter, with O being the midpoint.
- We can place L at (-5, 0) and M at (5, 0) on a coordinate plane for simplicity. Thus, O is at (0, 0).
- We know that:
- LP=6 cm
- MP=8 cm
- According to the Pythagorean theorem, in triangle LPM:
LP2+MP2=LM2
- Substitute the known lengths:
62+82=LM2
- Calculate the squares:
36+64=LM2
100=LM2
- Since we have already calculated LM=10 cm, we confirm:
LM2=102=100
- Since LP2+MP2=LM2, triangle LPM is a right triangle with the right angle at point P.
- According to the properties of circles, if a triangle is inscribed in a circle and one of its angles is a right angle, then the vertex of the right angle lies on the circumference of the circle.
- Therefore, point P lies on the circumference of the circle.
Point P lies on the circumference of the circle.
Topper's Solved these Questions
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - QUESTION BANK - 251videos
CIRCLES
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - QUESTION BANK - 261videos
CIRCLES
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AVERAGEEXERCISE - SELF ASSESSMENT SHEET10videos
AVERAGE
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Self Assessment Sheet10videos
CO-ORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
AB is a diameter of radius 4.5 cm circle. P is any point on the circumference of circle such that PN⊥AB. If length of chord PB is 6 cm . Then BN = ?
A5 cmB4 cmC6 cmD4.5 cm
In the figure, point P is the centre of the circle and line AB is the tangent to the circle at the point T. The radius of the circle is 6 cm . Find PB, if ∠TPB=60∘
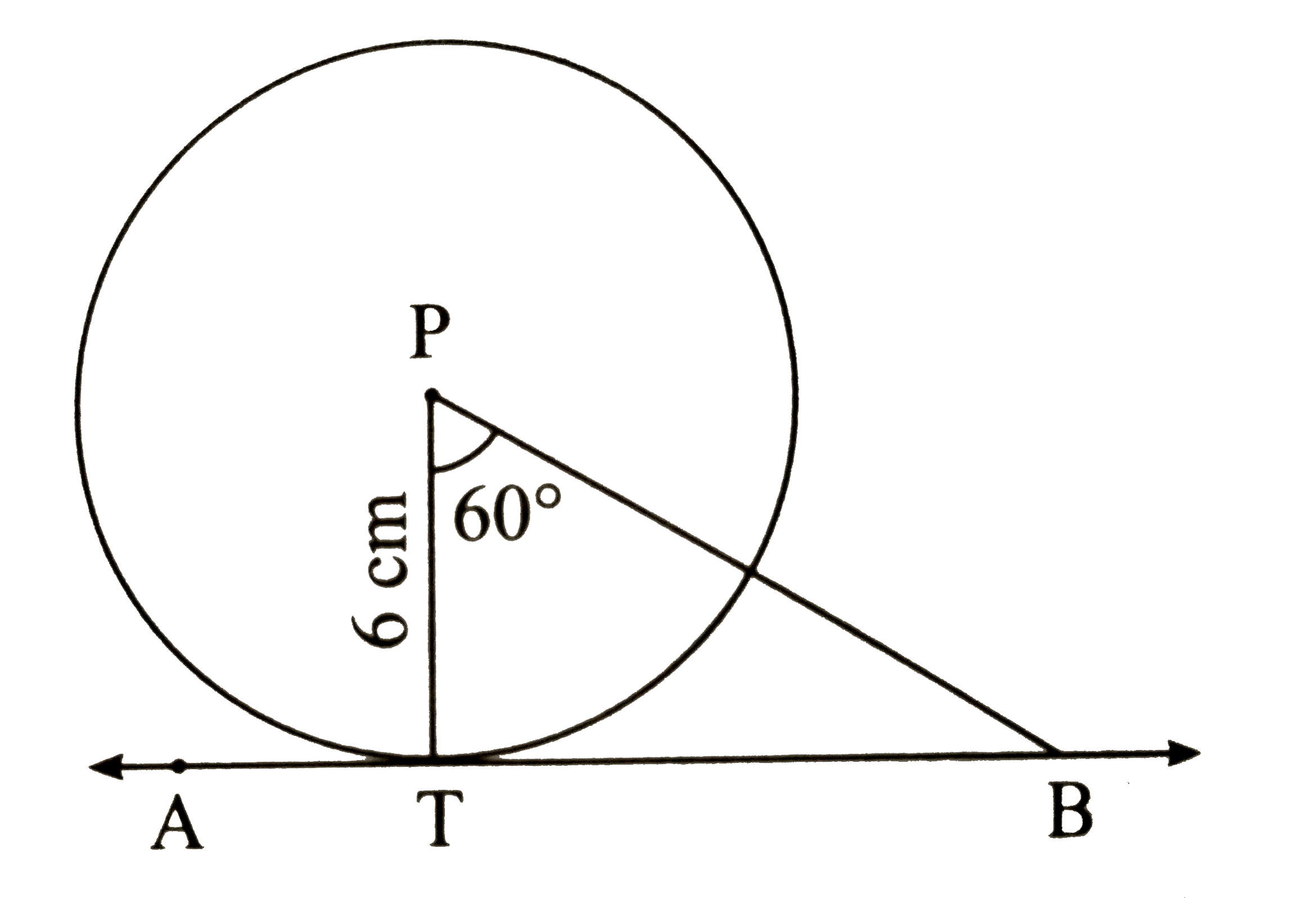 View Solution
View SolutionA line segment AB is the diameter of a circle with centre at O having radius 6.5 cm. Point P is in the plane of the circle such that AP=x and BP = y, In which one of the following cases the point P does not lie on the circle ?
View SolutionO is the centre of a circle of radius 8 cm. The tangent at a point A on the circle cuts a line through O at B such that AB=15cm . Find OB .
View SolutionP is a point out side a circle, which is 13 cm from the centre. A line drawn from point P intersects the circle at point A and B such that PA = 9 cm and AB = 7 cm. Then find the radius of the circle.
View SolutionA line through the centre O of a circle of radius 7 cm cuts the tangent, at a point P on the circle, at Q such that PQ=24cm . Find OQ .
View SolutionDraw a circle with radius 3.2 cm. Construct tangents to the circle from a point at a distance of 6 cm from the centre
View SolutionO is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E, find the length AB.
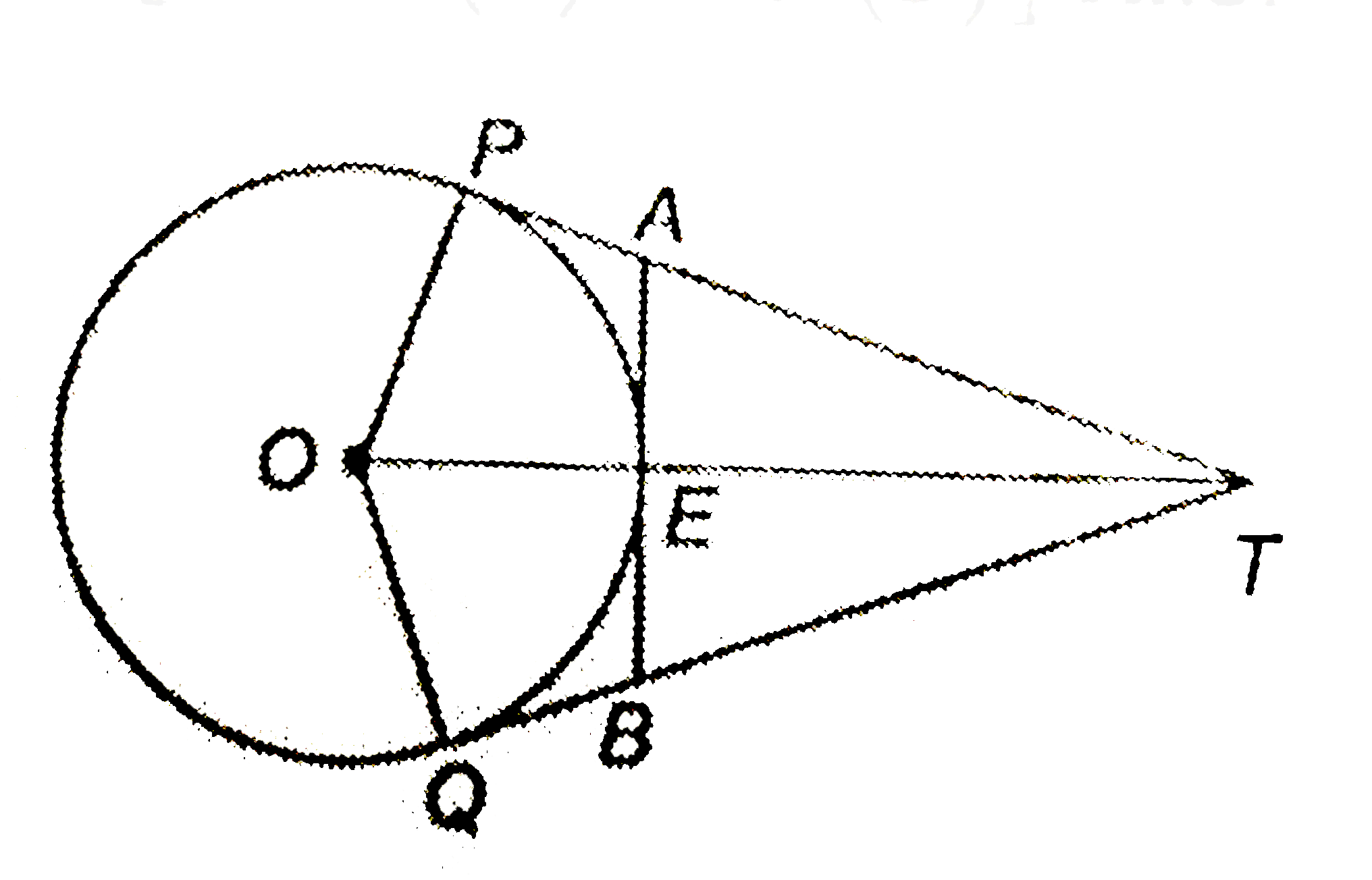 View Solution
View Solution

