O is the centre of the circle having radius 5 cm. AB and AC are two chords such that AB = AC = 6 cm. If OA meets BC at P, then OP =
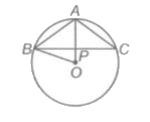
3.6 cm
1.4 cm
2 cm
3 cm
The correct Answer is:B
Step by step video & image solution for O is the centre of the circle having radius 5 cm. AB and AC are two chords such that AB = AC = 6 cm. If OA meets BC at P, then OP = by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLES BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - CIRCLES EXERCISE - Achievers Section (HOTS)
3 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Achievers Section (HOTS)
2 Videos
- CLASS 9 SAMPLE PAPER FINAL 4BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - CLASS 9 SAMPLE PAPER FINAL 4EXERCISE - MATHEMATICS
10 Videos
Similar Questions
Knowledge Check
There is a circle of radius 5 cm. There are two chords AB and AC OF equal length = 6 cm . Find the length of chord BC .
A4.8 cmB10.8cmC9.6 cmDnone of theseO is the centre of the circle of radius 6 cm and P is the mid -point of a chord AB .The length OP is 3 cm. The area (in sq cm ) of △AOB is :
A26πB24πC20πD18πIn the given figure, O is the centre of a circle of radius 13 cm and AB is a chord perpendicular to OD. If CD = 8 cm, then what is the length (in cm) of AB?
 AA)6 cmBB)12 cmCC)24 cmDD)28cm
AA)6 cmBB)12 cmCC)24 cmDD)28cm
In a circle of radius 5cm, AB and AC are two chords such that AB=AC=8 cm. What is the length of chord BC?
View SolutionIn a circle of radius 5cm, AB and AC are two chords such that AB=AC=6cm. The length of chord BC=
(A) 4.8cm
(B) 9.6cm
(C) 2.4cm
(D) 5cm
View SolutionIn a circle of radius 5 cm, AB and Ac are two chords of 6cm each. Find the length of the chord BC.
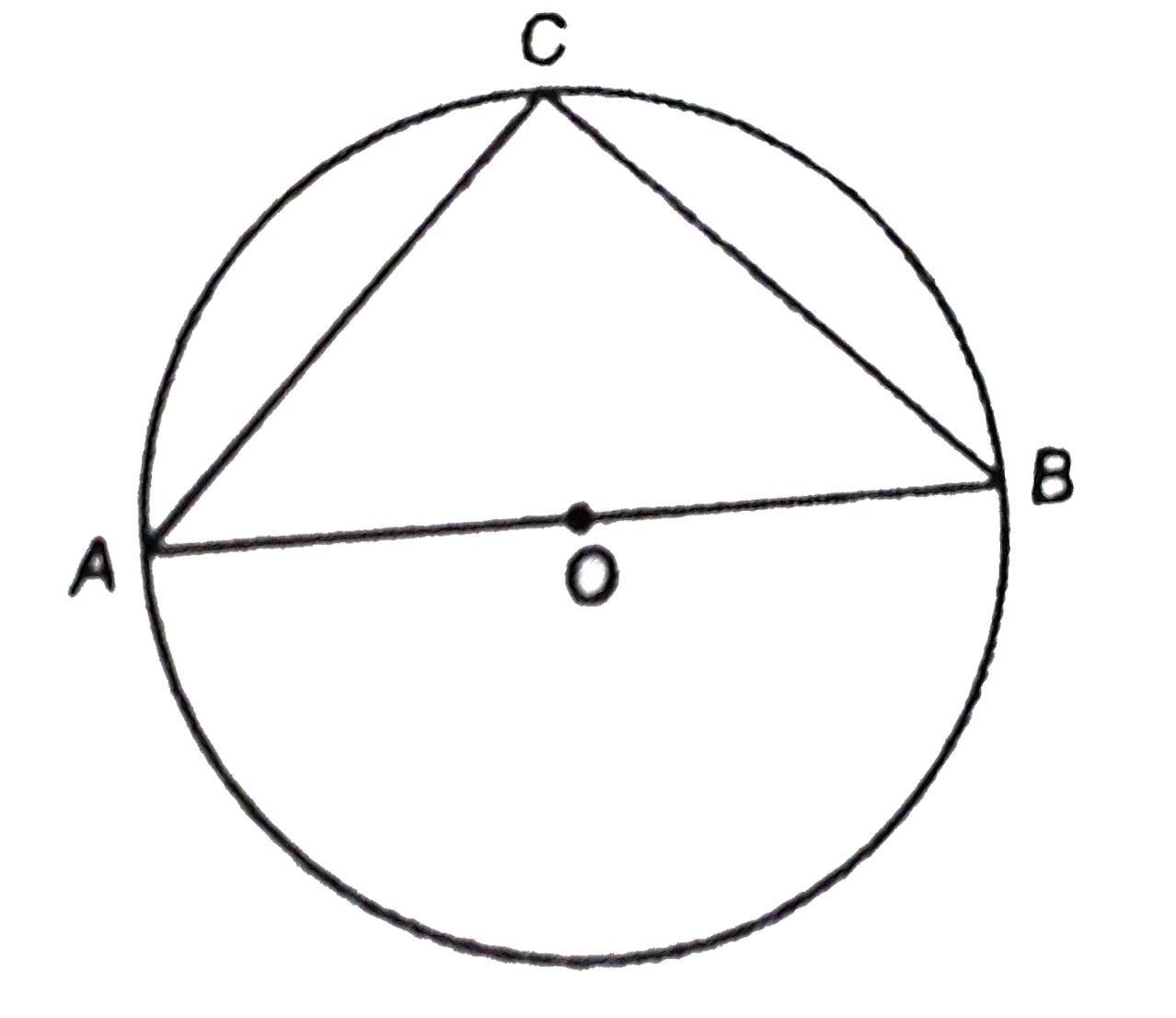
View SolutionO is the centre of a circle of diameter AB. If chord AC= chord BC, then find the value of ∠ABC.
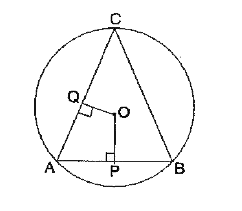
View SolutionO is the centre of the circle ABC, radius 5 cm, AB = 8 cm, AC = 6 cm. Calculate the lengths of the perpendiculars OP, OQ from O to AB, AC.
View Solution
