Question

${\displaystyle OPQR}$
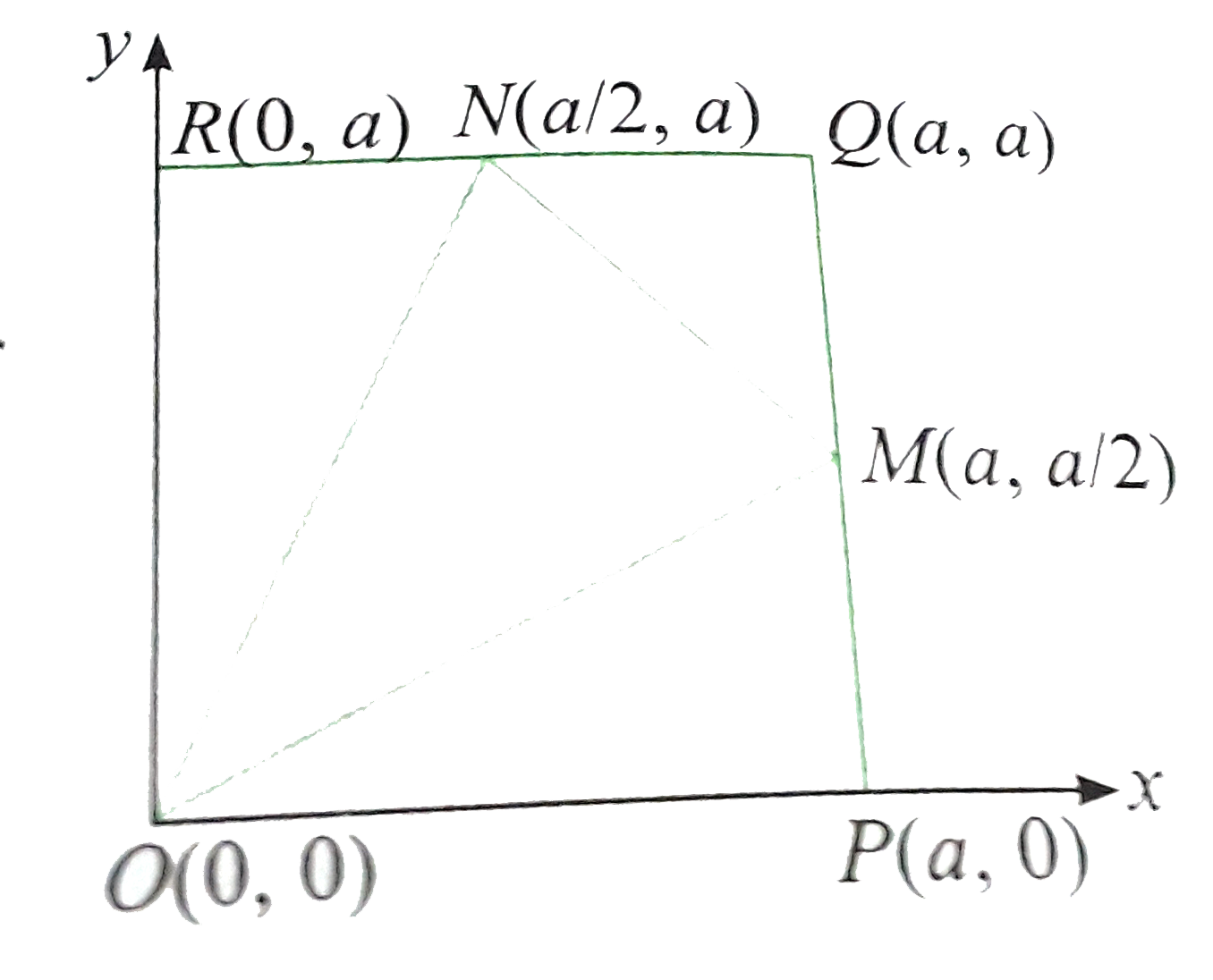
is a square and ${\displaystyle M,N}$
are the middle points of the sides ${\displaystyle PQandQR}$
, respectively. Then the ratio of the area of the square to that of
triangle ${\displaystyle OMN}$
is
4:1 (b) 2:1 (c) 8:3
(d) 7:3

Options

A. `4:1`
B. `2:1`
C. `8:3`
D. `7:3`

Answer

C

Explanation

Let the coordinates of vertices `O,P,Q,R` be `(0,0),(a,0)(a,a),(0,a)`, resepectively. Then we get the coordiantes of M as `(a,a//2)` and those of N as `(a//2,a)`. Therefore, the area of `DeltaOMA` is
`(1)/(2)|{:(0,,0,,1),(a,,a//2,,1),(a//2,,a,,1):}|=(3a^2)/(8)`
The area of the sqaure is `a^2`. Hence, the required ratio is `8:3`.