$O X$ and $O Y$ are two coordinate axes. On $O Y$ is taken a fixed point $P (0, c)$ and on $O X$ any point $Q .$ On $P Q,$ an equilateral triangle is described, its vertex $R$ being on the side of $P Q$ away from $O$ . Then prove that the locus of $R$ is $y = \sqrt{3} x - \cdot$

Video Solution

Text Solution

Verified by Experts

This given fixed point is $P (0, c)$ .
From given fig.,

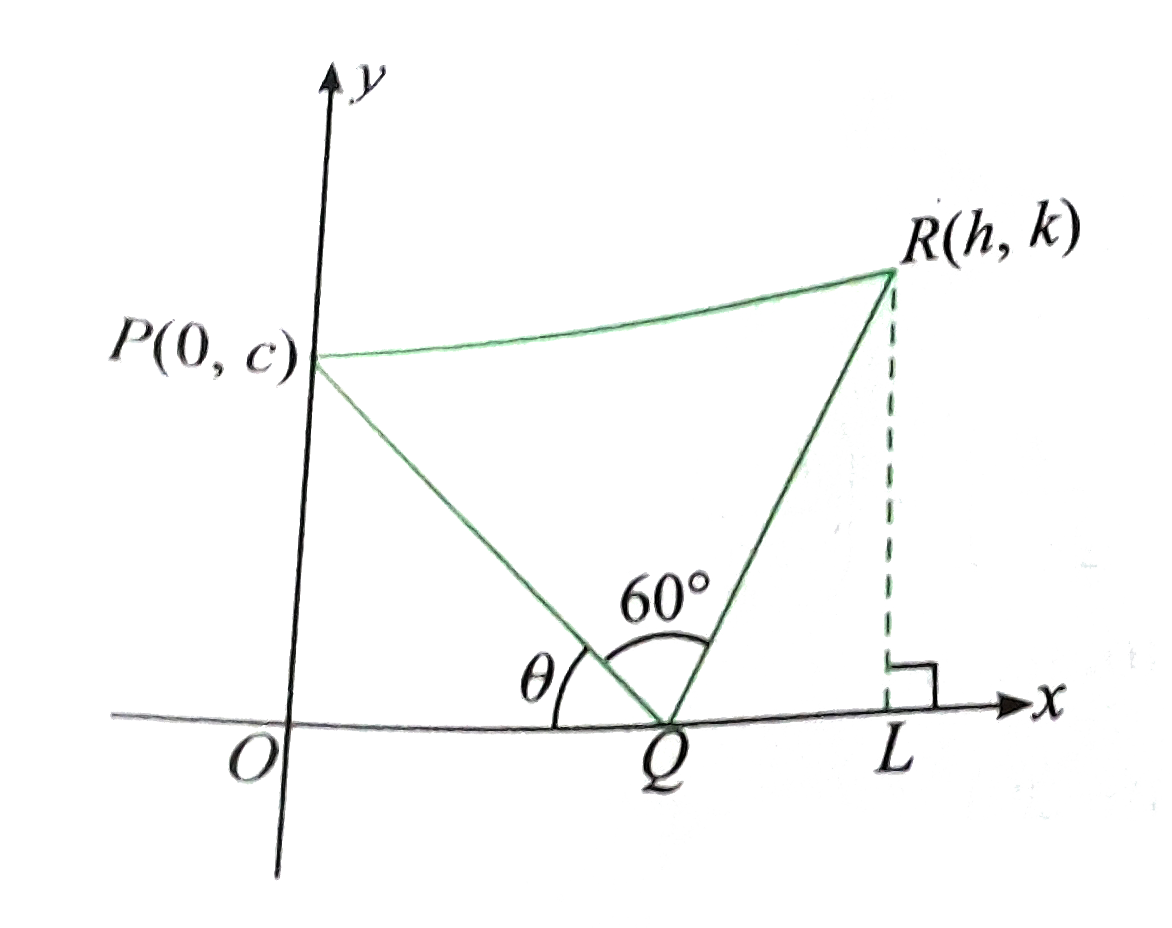
$h = O L = O Q + Q L$
$= c cot θ + Q r cos (180^{\circ} - 60^{\circ} - θ)$
$= c cot θ + P Q {{cos 120}^{\circ} . cos θ + {sin 120}^{\circ} . sin θ}$
$= c cot θ - \frac{P Q}{2} cos θ + \frac{\sqrt{3}}{2} P Q sin θ$
$= o t θ - \frac{1}{2} c cos e c θ cos θ + \frac{\sqrt{3}}{2} c cos e c θ sin θ [∵ sin θ = \frac{c}{P Q}]$
$∴ h = \frac{c}{2} (cot θ + \sqrt{3})$ (1)
Now, $k = R L = R Q sin (180^{\circ} - 60^{\circ} - θ)$
$= P Q {sin θ \times \frac{1}{2} + cos θ \times \frac{\sqrt{3}}{2}}$
$= c cos e c θ {\frac{1}{2} + sin θ \times \frac{\sqrt{3}}{2} cos θ}$
$∴ k = \frac{c}{2} (1 + \sqrt{3} cot θ)$
Eliminating $cot θ$ from (1) and (2) , we get $k = \sqrt{3} h - c$ .
Therefore the required locus is $y = \sqrt{3} x - c$ , a straight line.

Updated on:21/07/2023