Obtain the equivalent simple circuits of the following switching circuits :
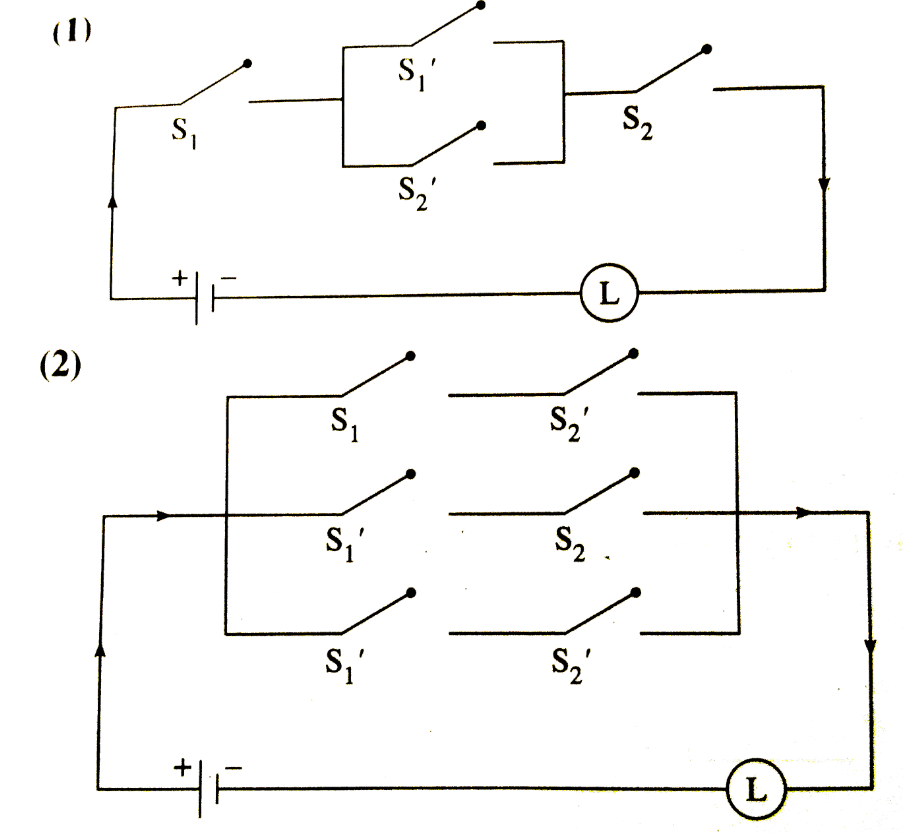
Text Solution
Let p : the switch S1 is closed
q : the switch S2 is closed
~p : the switch S1' is closed or the switch S1 is open
~q : the switch S2' is closed or the switch S2 is open
(1) The symbolic form of given circuit is : p∧(~p∨~q)∧q Using the laws of logic, we have,
p∧(~p∨~q)∧q
≡[p∧(~p∨~q)]∧q ...... By Associative Law
≡[(p∧~p)∨(p∧~q)]∧q ...... By Distributive Law
≡[F∨(p∧~q)]∧q ...... By Complement Law
≡(p∧~q)∧q By Identity Law
≡p^^(~q^^q)" "......ByAssociativeLaw<br>-=p^^F" "......Bycomp≤mentLaw<br>-=F" ".......ByIdentityLaw<br>:.the∘uitwill≠verworkanditwillbealwaysoffirrespectiveofthestatusofswitches.<br>(2)Thesymbolicformofthegiven∘uitis:(p^^~q)vv(~p^^q)vv(~p^^~q)Usingthelawsoflogic,wehave,<br>(p^^~q)vv(~p^^q)vv(~p^^~q)<br>-=(p^^~q)vv[(~p^^q)vv(~p^^~q)]" "......ByAssociativeLaw<br>-=(p^^~q)vv[~p^^(qvv~q)]" "......ByDistributiveLaw<br>-=(p^^~q)vv(~p^^T)" "......ByComp≤mentLaw<br>-=(p^^~q)vv~p" "......ByIdentityLaw<br>-=(pvv~p)^^(~qvv~p)" "......ByDistributiveLaw<br>-=T^^(~qvv~p)" "......ByComp≤mentLaw<br>-=~qvv~p" "......ByIdentityLaw<br>-=~pvv~q" "...... By Commutative Law
Hence, the simplified circuit of the given circuit is :
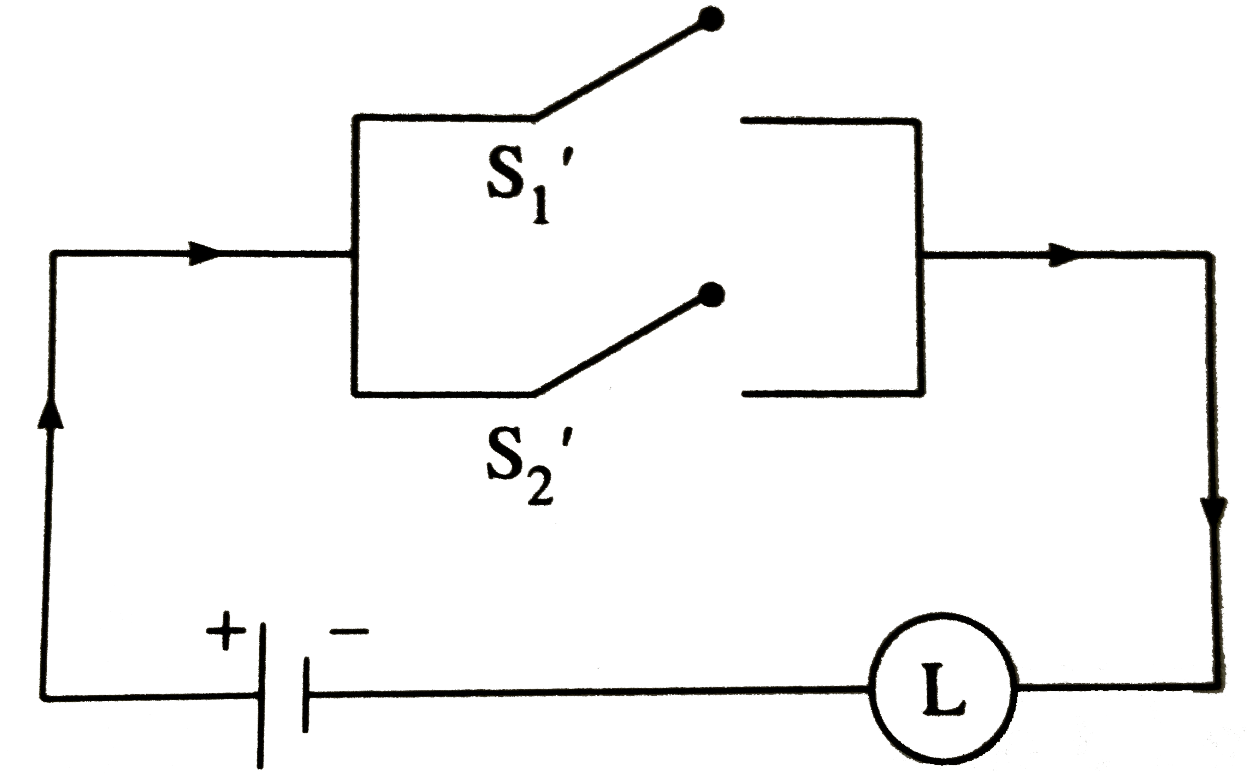
|
Topper's Solved these Questions
- MATHEMATICAL LOGICBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MATHEMATICAL LOGICEXERCISE - EXAMPLES FOR PRACTICE 2 OR 3 MARKS EACH
24 Videos
- MATHEMATICAL LOGICBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MATHEMATICAL LOGICEXERCISE - EXAMPLES FOR PRACTICE 3 MARKS EACH
4 Videos
- LINEAR PROGRAMMING BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINEAR PROGRAMMING EXERCISE - EXAMPLES FOR PRACTICE
8 Videos
- MATRICESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MATRICESEXERCISE - MULTIPLE CHOICE QUESTIONS
12 Videos
Similar Questions
Knowledge Check
What is equivalent resistance on the circuit shown in the given circuit ?
 A13ΩB37ΩC3013ΩD270Ω
A13ΩB37ΩC3013ΩD270Ω
Find equivalent resistance in each of the following circuits :
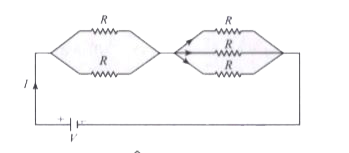
View SolutionFind equivalent resistance in each of the following circuits :
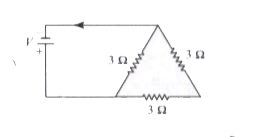
View SolutionFind equivalent resistance in each of the following circuits :
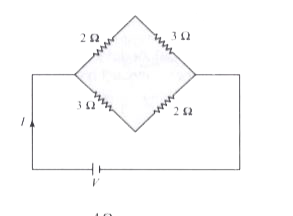
View SolutionFind equivalent resistance in each of the following circuits :
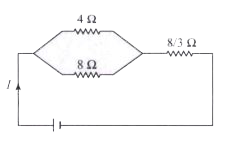
View SolutionSwitching and RC Circuits
View SolutionFind the equivalent resistance between A and B in the following circuit.

View Solution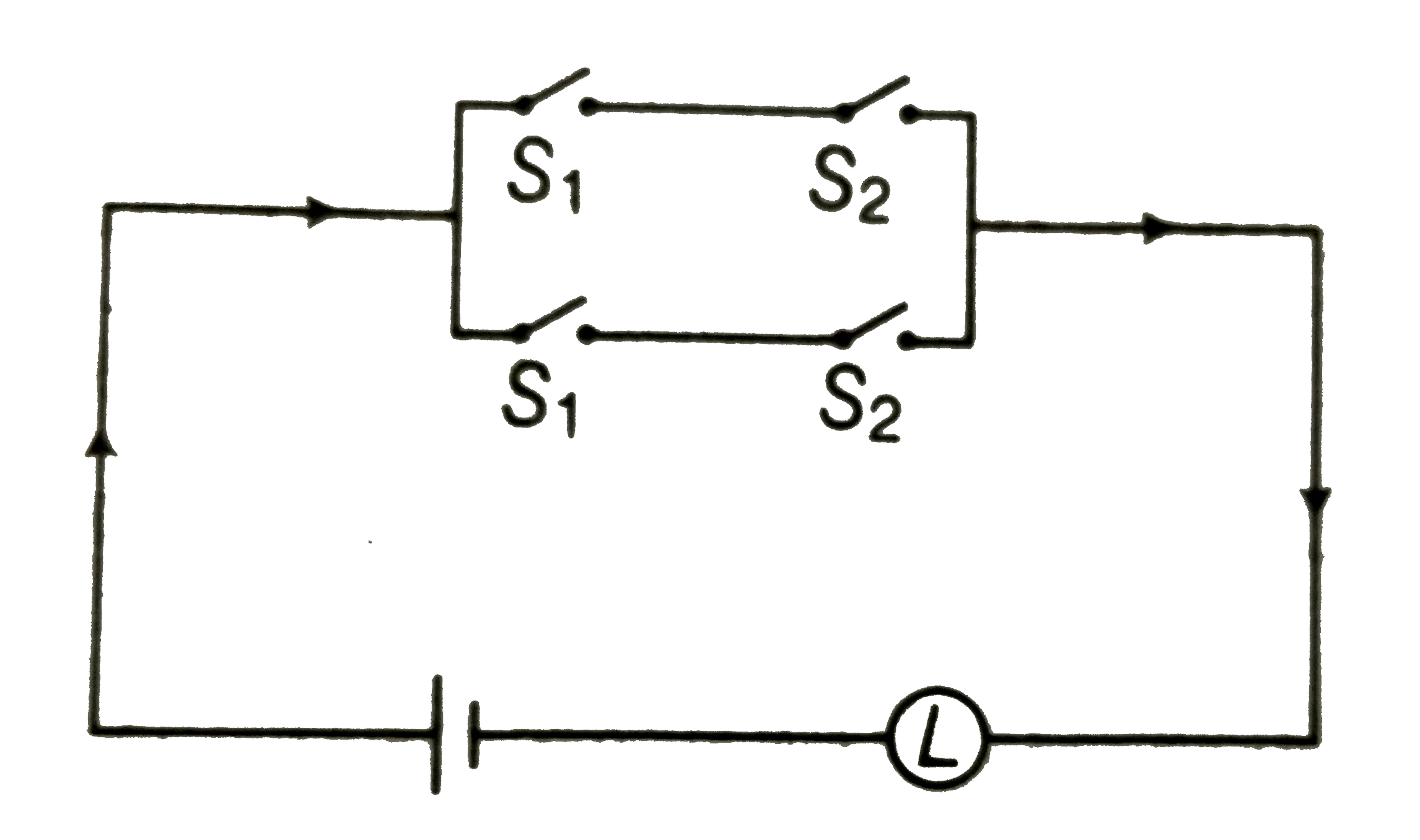
Symbolic form of the given switching circuit is equivalent to
View Solution


