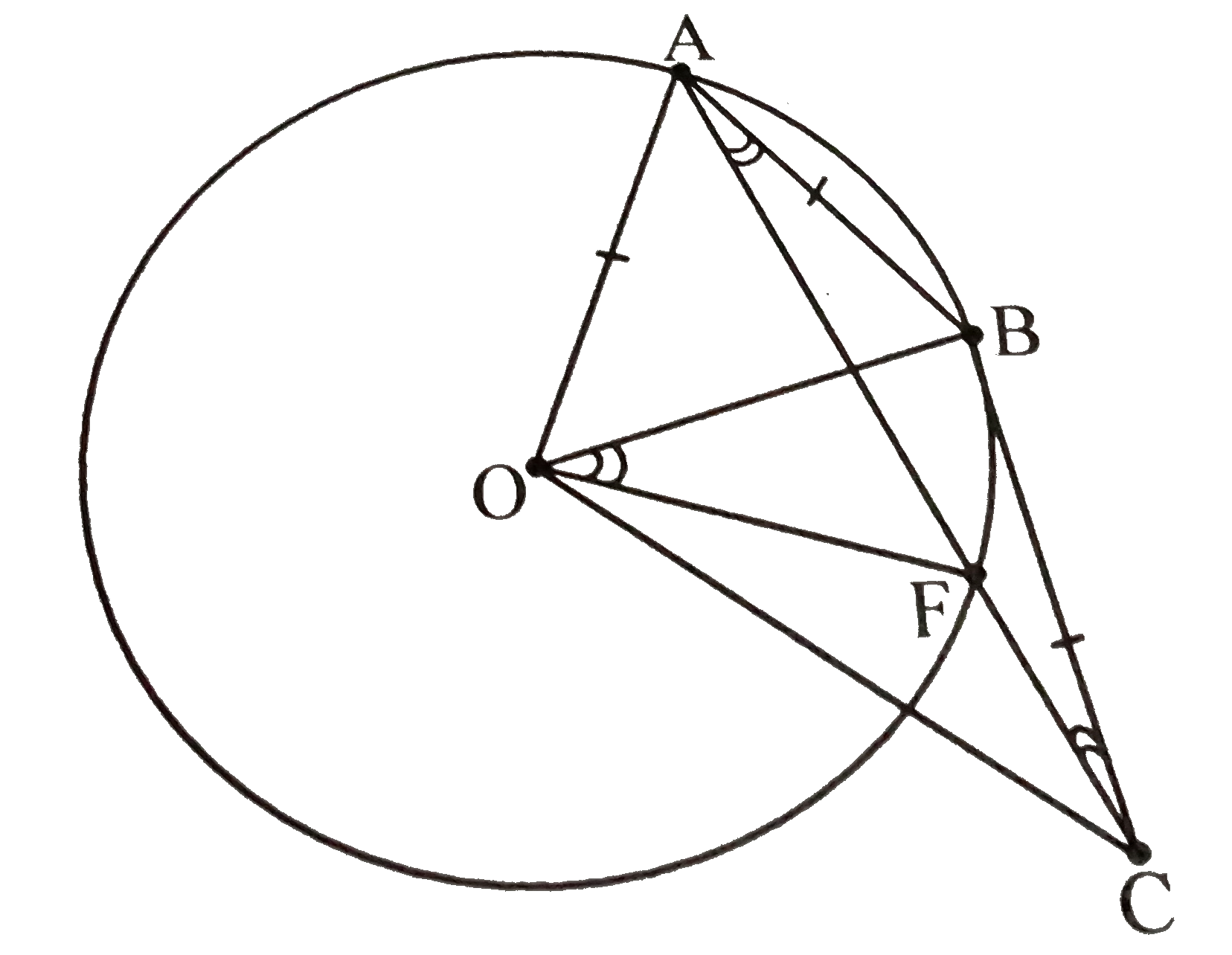
On the circle with centre O, points A, B are such that OA =AB. A point C is located on the tangent at B to the circle such that A and C are on the opposite sides of the line OB and Ab =BC. The line segment AC intersects the circle again at F. Then the ratio ∠BOF:∠BOC is equal to-
1:2
2:3
3:4
4:5
The correct Answer is:B
∴ΔOAB should be equilareral
Now ∠OBC=90∘&AB=BC
⇒∠BAC=∠BCA=15∘
∴Ang≤BOF=30∘&∠BOC=45∘ {Delta OBCisrightisosce≤s}
∴∠BOF∠BOC=30∘45∘=23 {∠BOF=2∠BAF}
Topper's Solved these Questions
Similar Questions
Knowledge Check
AB and AC are tangents to the circle with centre O. Then x equals.
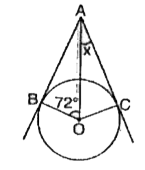A22∘B18∘C20∘D36∘PA and PB are two tangents to a circle with centre O, from a point P outside the circle . A and B are point P outside the circle . A and B are point on the circle . If ∠PAB=47∘ , then ∠OAB is equal to :
A43∘B53∘C50∘D20∘In the given figure, AB and AC are tangents to the circle at B and C respectively and O is the centre of the circle, then x equals
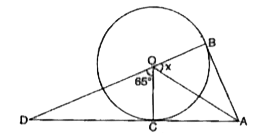A65∘B32.5∘C57.5∘D45∘
Points A and B are on a circle of radius 5 and AB = 6. Point C is the midpoint of the minor arc AB length of the line segement AC, is:
View SolutionIf A. B and C are three points on a line, and B lies between A and C then prove that AB−BC=AC.
View SolutionA circle centred at O has radius 1 and contains the point A. Segment AB is tangent to the circle at A and angle AOB=θ.If point C lies on OA and BC bisects the angle ABO then OC equals
View SolutionA circle centred at O has radius 1 and contains the point A. Segment AB is tangent to the circle at A and angle AOB=θ.If point C lies on OA and BC bisects the angle ABO then OC equals
View SolutionIn the figure, point P is the centre of the circle and line AB is the tangent to the circle at the point T. The radius of the circle is 6 cm . Find PB, if ∠TPB=60∘
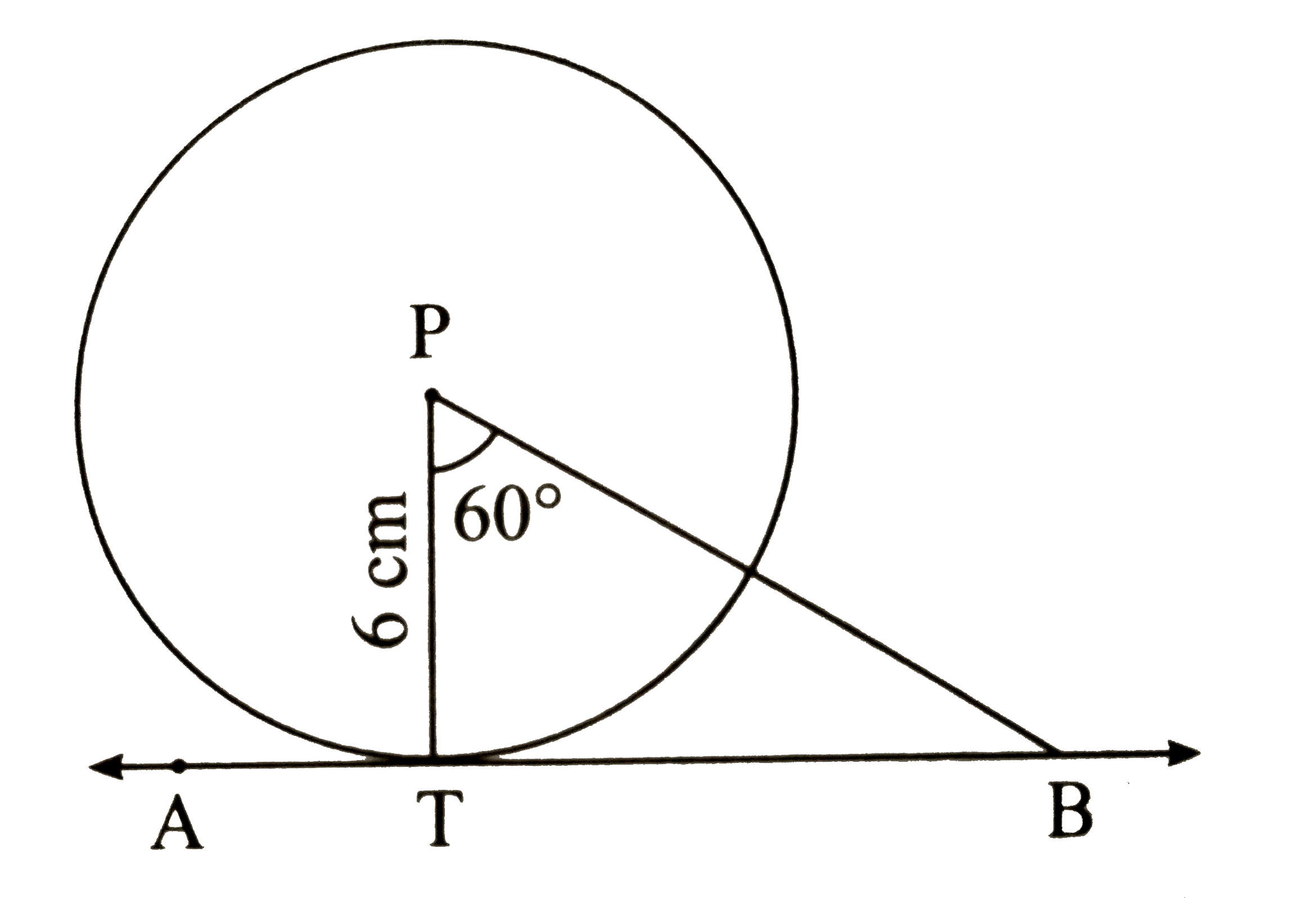
View Solution