One side of a parallelogram is 10 cm. If its diagonals are 12 cm and 16 cm. Find the area of the parallelogram.
The correct Answer is:96cm2
To find the area of the parallelogram given one side and the lengths of its diagonals, we can follow these steps:
Step 1: Understand the properties of the parallelogram
We know that the diagonals of a parallelogram bisect each other. This means that if we label the diagonals as AC and BD, they will intersect at point O.
Step 2: Label the given information
- Let AB=CD=10cm (one side of the parallelogram).
- Let BD=12cm (one diagonal).
- Let AC=16cm (the other diagonal).
Step 3: Find the lengths of the segments formed by the diagonals
Since the diagonals bisect each other:
- BO=OD=BD2=122=6cm
- AO=OC=AC2=162=8cm
Step 4: Calculate the area of triangle COD
The area of triangle COD can be calculated using the formula:
Area=12×base×height
Here, the base CD=10cm and the height H is unknown. So, we can express the area as:
AreaCOD=12×10×H=5Hcm2
Step 5: Use Heron's formula to find the area of triangle COD
Using Heron's formula, we first calculate the semi-perimeter s:
s=AO+BO+CD2=8+6+102=12cm
Now, we can apply Heron's formula:
Area=√s(s−a)(s−b)(s−c)
Where a=10cm, b=6cm, and c=8cm:
AreaCOD=√12×(12−10)×(12−6)×(12−8)
Calculating this:
=√12×2×6×4=√576=24cm2
Step 6: Set the areas equal to find height H
From Step 4 and Step 5, we have:
5H=24
Solving for H:
H=245=4.8cm
Step 7: Calculate the height of the parallelogram
Since the height of the triangle COD is half the height of the parallelogram, the total height h of the parallelogram is:
h=2H=2×4.8=9.6cm
Step 8: Calculate the area of the parallelogram
The area A of the parallelogram is given by:
A=base×height=10×9.6=96cm2
Final Answer
The area of the parallelogram is 96cm2.
---
We know that the diagonals of a parallelogram bisect each other. This means that if we label the diagonals as AC and BD, they will intersect at point O.
- Let AB=CD=10cm (one side of the parallelogram).
- Let BD=12cm (one diagonal).
- Let AC=16cm (the other diagonal).
Since the diagonals bisect each other:
- BO=OD=BD2=122=6cm
- AO=OC=AC2=162=8cm
The area of triangle COD can be calculated using the formula:
Area=12×base×height
Here, the base CD=10cm and the height H is unknown. So, we can express the area as:
AreaCOD=12×10×H=5Hcm2
Using Heron's formula, we first calculate the semi-perimeter s:
s=AO+BO+CD2=8+6+102=12cm
Now, we can apply Heron's formula:
Area=√s(s−a)(s−b)(s−c)
Where a=10cm, b=6cm, and c=8cm:
AreaCOD=√12×(12−10)×(12−6)×(12−8)
Calculating this:
=√12×2×6×4=√576=24cm2
From Step 4 and Step 5, we have:
5H=24
Solving for H:
H=245=4.8cm
Since the height of the triangle COD is half the height of the parallelogram, the total height h of the parallelogram is:
h=2H=2×4.8=9.6cm
The area A of the parallelogram is given by:
A=base×height=10×9.6=96cm2
The area of the parallelogram is 96cm2.
Topper's Solved these Questions
- HERONS'S FORMULABOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - HERONS'S FORMULAEXERCISE - Revision Exercise
11 Videos
- HERONS'S FORMULABOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - HERONS'S FORMULAEXERCISE - Exercise 12a
11 Videos
- CONSTRUCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE
36 Videos
- INTRODUCTION TO EUCLID'S GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INTRODUCTION TO EUCLID'S GEOMETRYEXERCISE - Exercise
8 Videos
Similar Questions
Knowledge Check
The adjacent sides of a parallelogram are in the ratio 5:3. if its perimeter is 96cm, find the sides of the parallelogram.
A30cm and 18cm.B55cm and 18cm.C26cm and 10cm.D37cm and 28cm.
One side of a parallelogram is 20cm and its distance from the opposite side is 16cm. Find the area of the parallelogram.
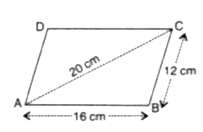
View SolutionIn parallelogram ABCD, AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram.
View SolutionTwo adjacent sides of a parallelogram are 28 cm and 26 cm. If one diagonal of it is 30 cm long, Find the area of the parallelogram. Also, find the distance between shorter sides.
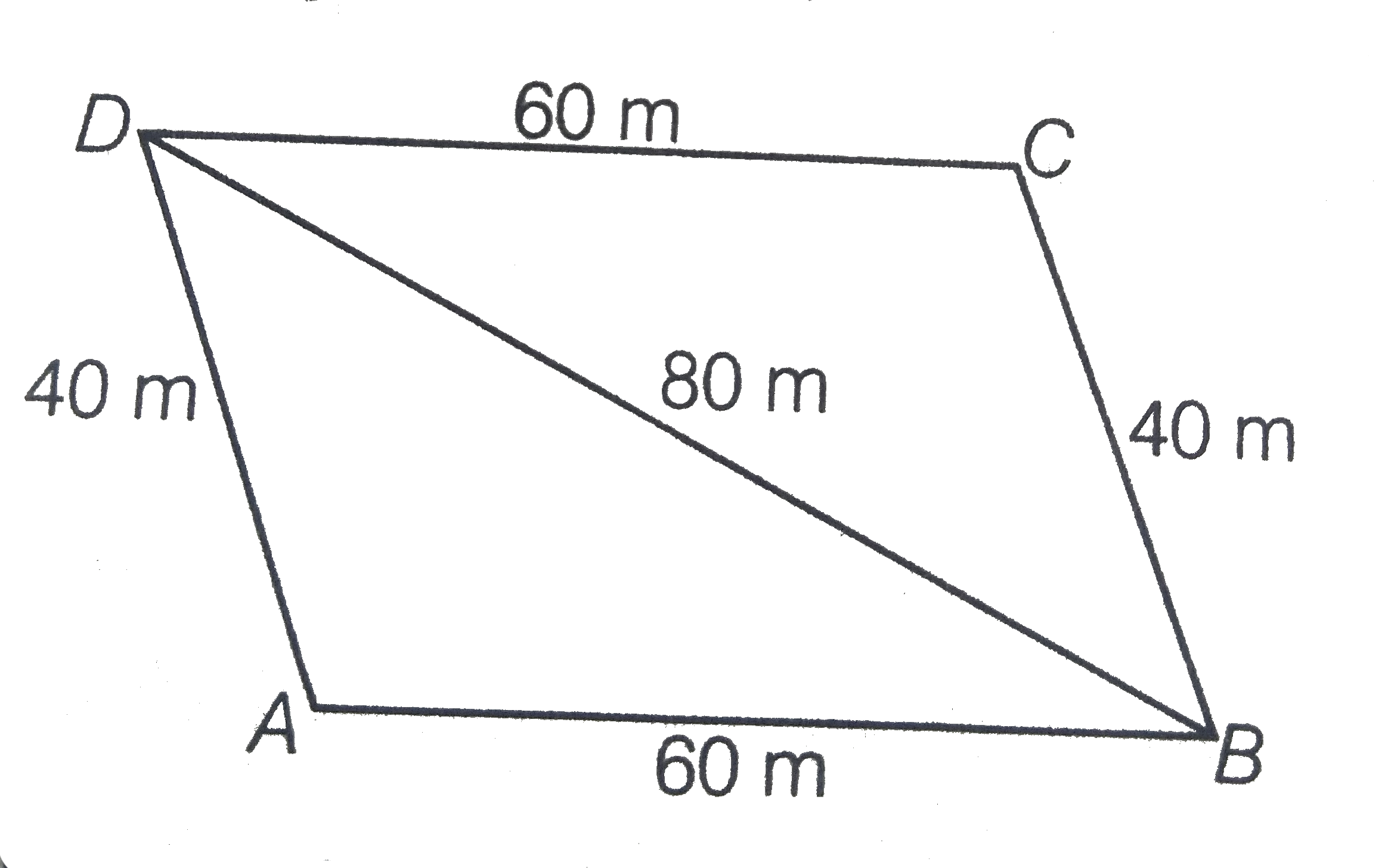
View SolutionA field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
View SolutionOne of the sides and the corresponding height of a parallelogram are 4 cm and 3 cm respectively. Find the area of the parallelogram (Fig 11.17).
View SolutionThe lengths of the diagonals of a rhombus are 12 cm and 16 cm. Find the area of rhombus
View SolutionThe side of a rhombus is 15cm. If its one diagonal is 18 cm. Find its area.
View Solution
