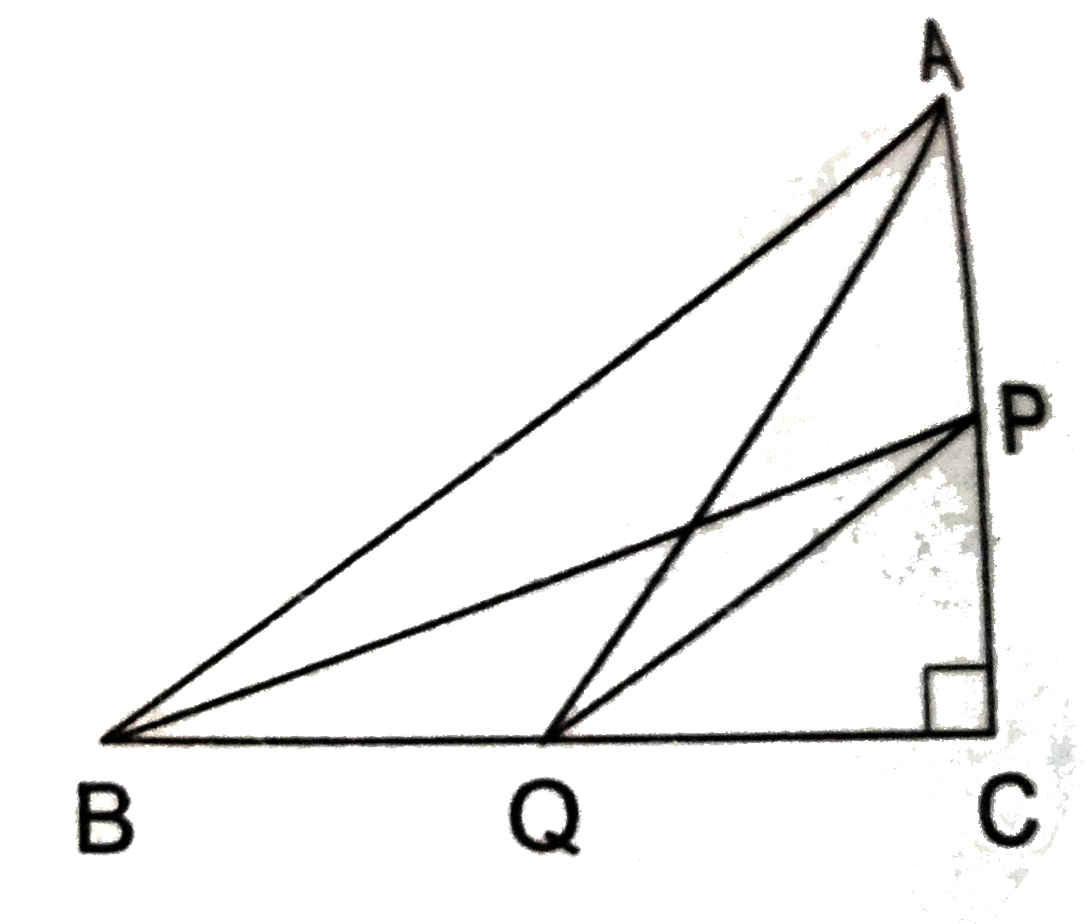
P and Q are points on the sides CA and CB respectively of ABC , right angled at C . Prove that AQ2+BP2=AB2+PQ2 .
GIVEN AΔABC in which ∠C=90∘.
P and Q are points on CA and CB repectively.
TO PROVE (AQ2+BP2)=(AB2+PQ2)
PROOF From fight ΔACQ, we have
AQ2=(AC2+CQ2) ....(i) [ by Pythagora's thoerem]
From right ΔBCP, we have
BP2=(BC2+CP2) ....(ii) [ by Pythagora's thoerem]
From right ΔACB, we have
AB2=AC2+BC2 ....(iii) [ by Pythagora's thoerem]
From right ΔPCQ, we have
PQ2=(CQ2+CP2) ....(i) [ by Pythagora's thoerem]
From (i) and (ii), we get
(AQ2+BP2)=(AC2+BC2)+(CQ2+CP2)
=(AB2+PQ2) [ using (iii ) and (iv)]
Hence, (AQ2+BP2)=(AB2+PQ2)
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Knowledge Check
P and Q are points on the sides CA and CB respectively of ABC , right angled at C . Prove that AQ2+BP2=AB2+PQ2 .
ABC2+PQ2BAB2+PC2CAB2+PQ2DBC2+AC2
In a ABC , P and Q are point on the sides AB and AC respectively, such that PQBC . If AP=2.4cm , AQ=2cm , QC=3cm and BC=6cm , find AB and PQ .
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View SolutionIn Figure, XandY are the mid-points of ACandAB respectively, QP,BCandCYQandBXP are straight lines. Prove that ar(ABP)=ar(ACQ)
View SolutionIn ABC , P and Q are points on sides AB and AC respectively such that PQBC . If AP=4cm, PB=6cm and PQ=3cm , determine BC .
View SolutionIn a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
View SolutionIn ABC , points P and Q are on CA and CB , respectively such that CA=16cm , CP=10cm , CB=30cm and CQ=25cm . Is PQ∣∣AB ?
View Solution
