In Figure, XandY are the mid-points of ACandAB respectively,
QP,BCandCYQandBXP are straight lines. Prove that ar(ABP)=ar(ACQ)
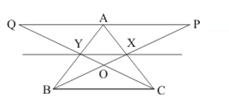
Step by step video & image solution for In Figure, X and Y are the mid-points of AC and A B respectively, QP, BC and CYQ and BXP are straight lines. Prove that ar (ABP)=ar (ACQ) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In figure X and Y are the mid-points of AC and AB respectively, QP∣∣BC and CYQ and BXP are straight lines. Prove that ar(ΔABP)=ar(ΔACQ).
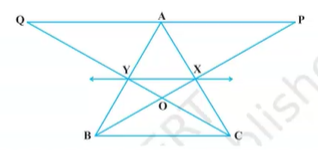
View SolutionIn Figure, XandY are the mid-points of ACandAB respectively, QP,BCandCYQandBXP are straight lines. Prove that ar(ABP)=ar(ACQ)

View SolutionIn the adjoining figure D, E and F are the mid - points of the sides BC, AC and AB respectively to triangle. Show that ∠EDF=∠A, ∠DEF=∠B and ∠DFE=∠C:

View SolutionIn ΔABC , if L and M are the points on AB and AC, respectively such that LM∣∣BC. Prove that ar(ΔLOB)=ar(ΔMOC).
View SolutionD and E are points on sides AB and AC respectively of ΔABC such that ar(ΔDBC) = ar(ΔEBC). Prove that DE I I BC.
View SolutionIn the adjoining figure , we have X and Y are the mid - point of AC and BC and AX = CY . Show that AC =BC.
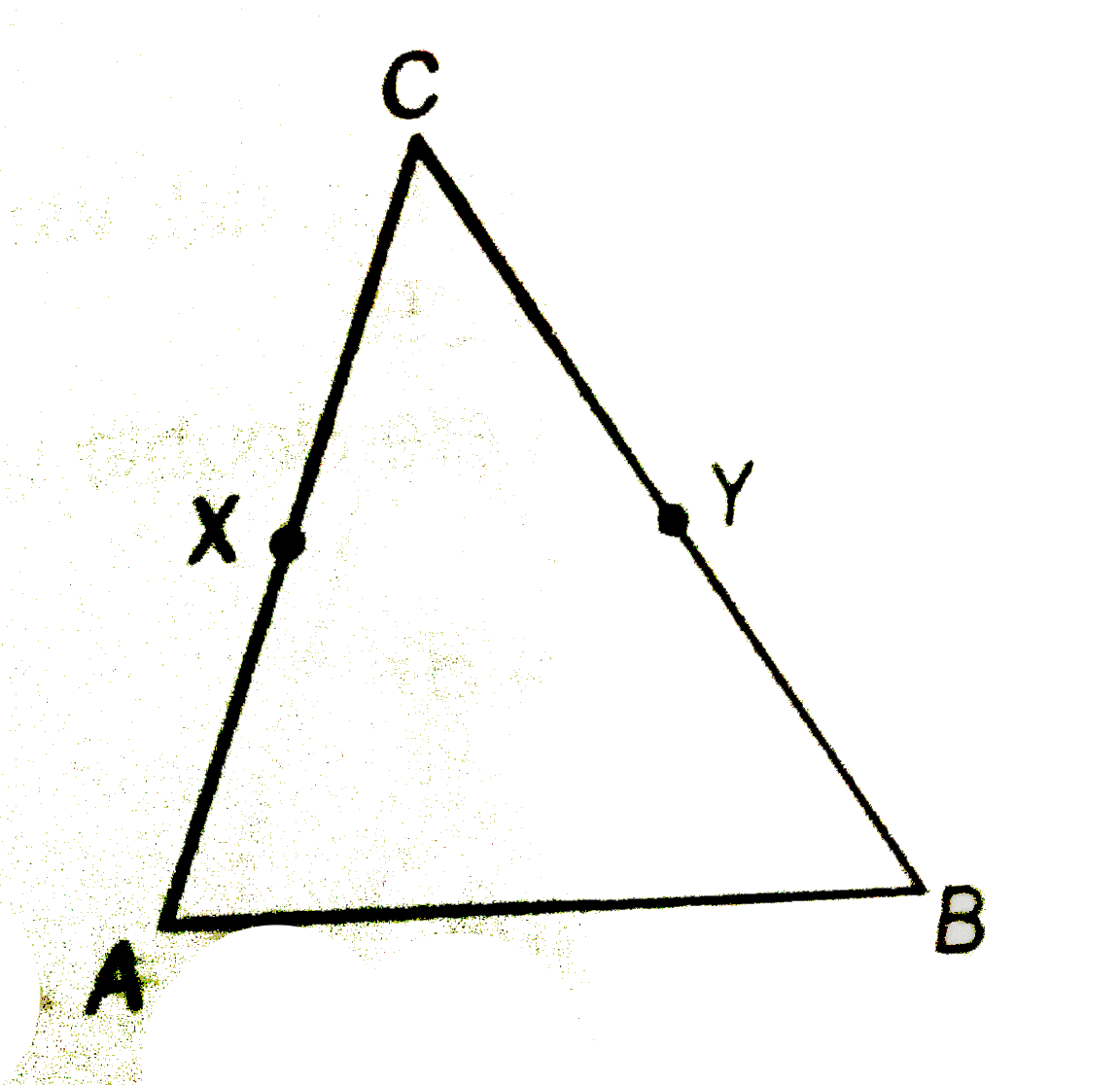
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, AC and AB respectively. △DEF is congruent to triangle :

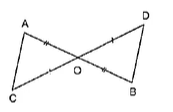
View SolutionIn Figure O is the mid-point of AB and CD. Prove that AOC≅ BOD (b) AC=BD (iii) AC∣∣BD
View SolutionIn trapezium ABCD, AB∣∣DC and L is the mid-point of BC. Through L, a line PQ∣∣AD has been drawn which meets AB in P and DC produced in Q. Prove that ar (ABCD) = ar (APQD).

View SolutionIf B is the mid point of ACandC is the mid point of BD,whereA,B,C,D lie on a straight line, say why AB=CD?
View Solution
