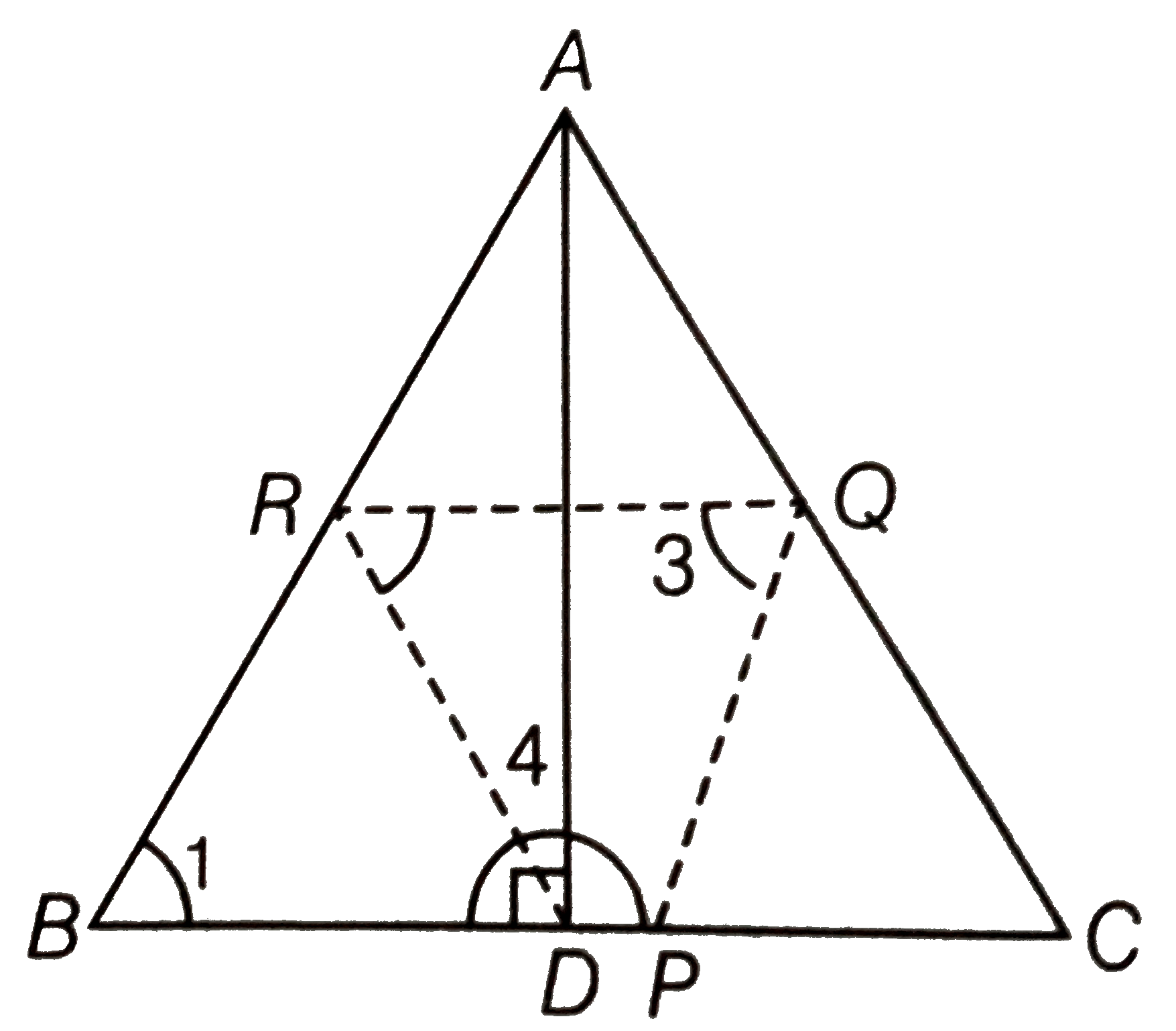
are, respectively, the mid points of sides of a triangle
Given In , P, Q and R are the mid-points of the sides BC, CA and AB respectively Also, .
To prove P, Q, R and D are concyclic.
Construction Join DR, RQ and QP
Proof In right angled , R is the mid-point of AB.
....(i)
[angles opposite to the equal sides are equal]
Since, R and Q are the mid-point of AB and AC, then
[by mid-point theorem]
or
Since,then quadrilateral BPQR is a parallelogram.
..(ii)
[opposite angles of parallelogram are equal]
from Eqs. (i) and (ii),
But [linear pair axiom]
Hence, quadrilateral PQRD is a cyclic quadrilateral.
So, points P, Q, R and D are con-cyclic.
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
In ABC, D, E and F are, respectively, the mid-points of BC, CA and AB . If the lengths of side AB, BC and CA are 7cm, 8cm, and 9cm, respectively, find the perimeter of DEF
View SolutionIn Figure, BE⊥AC, AD is any line from A → BC intersecting BE in H.P, Q and R are respectively the mid-points of AH, AB and BC. Prove that ∠PQR=900
View SolutionIn a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC=21 cm, BC=29cm and AB=30cm, find the perimeter of the quadrilateral ARPQ
View SolutionD and E are, respectively, the points on equal sides AB and AC of an isosceles triangle ABC such that B, C, E, and D are concyclic as shown in Figure. If O is the point of intersection of CD and BE, prove that AO is the bisector of line segment DE
View SolutionGiven ABC , lines are drawn through A, B and C parallel respectively to the sides BC, CA and AB, forming PQR.Figure .Show that BC=12QR
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that (i) ar(PRQ)=12ar(ARC)(ii) ar(RQC)=38ar(ABC)(iii) ar(PBQ)=ar(ARC)
View SolutionIn A ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (RQC)=38 ar ( ABC)
View SolutionIn A ABC , P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar(PRQ)=12ar(ARC)
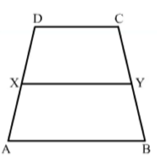
View SolutionIn Figure, ABCD is a trapezium in which AB,DCandDC=40cmandAB=60cm If XandY are, respectively, the mid-points of ADandBC, prove that: ar(traptDCYX)=911,ar(trap(XYBA)
View SolutionD, E, F are the mid-point of the sides BC, CA and AB respectively of ABC. Then DEF is congruent to triangle. ABC (b) AEF (c) BFD, CDE (d) AFE, BFD, CDE
Given : D, E, F are the mid-point of the sides BC, CA and AB .
View Solution
