Parameters of binomial distribution of variable X are 2n+1 and p=12. Then …….. Is the probability that random variable X takes odd numbers.
A
12
B
12n
C
12n+1
D
32
Text Solution
The correct Answer is:A
|
Topper's Solved these Questions
- PROBABILITYBOOK - KUMAR PRAKASHANCHAPTER - PROBABILITYEXERCISE - Practice Paper - 13 (Section - A (Choose the correct option))
6 Videos
- PROBABILITYBOOK - KUMAR PRAKASHANCHAPTER - PROBABILITYEXERCISE - Practice Paper - 13 (Section - B (Answer the following questions))
4 Videos
- PROBABILITYBOOK - KUMAR PRAKASHANCHAPTER - PROBABILITYEXERCISE - Solutions of NCERT Exemplar Problems (Fillers)
5 Videos
- MATRICES BOOK - KUMAR PRAKASHANCHAPTER - MATRICES EXERCISE - Practice Paper - 3 (Section - D)
1 Videos
- RELATIONS AND FUNCTIONS BOOK - KUMAR PRAKASHANCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Practice Paper - 1 (Section - D)
2 Videos
Similar Questions
Knowledge Check
If mean and variance of a Binomial variate X are 2 and 1 respectively, then the probability that X takes a value greater than 1 is:
A516B816C1116D116Which of the following distribution of probabilities of a random variable X is the probability distribution ?
A B
B C
C D
D
If X has a binomial distribution, B(n, p) with parameters n and p such that P(X = 2) = P(X = 3), then E(X), the mean of variable X, is
A2-pB3-pCp/2Dp/3
If X has a binomial distribution, B(n,p) with parameters n and p such that P(X=2)=P(X=3), then E(X) , the mean of variable X, is
View SolutionThe probability distribution of a random variable X is given as
Then, the value of p is
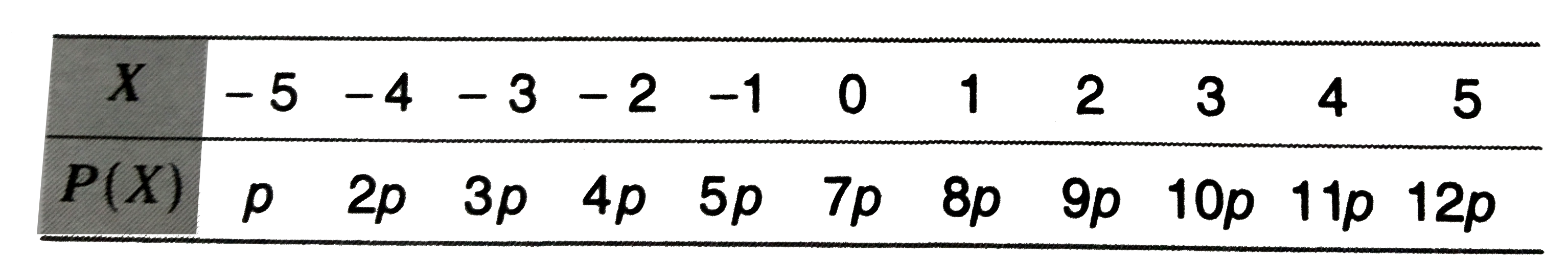
View SolutionA random variable Xtakes the values0,1and2.If P(X=1)=P(X=2)andP(X=0)=0.4,then the mean value of the random variableX is
View SolutionThe probability distribution of a random variable is as follows: The variance of x is
View SolutionA binomial random variable X, 5P(X = 3) = 2P(X = 2), when n = 5. Find the value of parameter p.
View Solution


