Random variable X takes integer values from 1 to n with equal probabilities then E(X)=……….. Solution in Gujrati
n2
0
n−12
n+12
The correct Answer is:D
Step by step video, text & image solution for Random variable X takes integer values from 1 to n with equal probabilities then E(X) = ……….. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - PROBABILITYEXERCISE - Practice Paper - 13 (Section - A (Choose the correct option))6videos
PROBABILITY
- BOOK - KUMAR PRAKASHANCHAPTER - PROBABILITYEXERCISE - Practice Paper - 13 (Section - B (Answer the following questions))4videos
PROBABILITY
- BOOK - KUMAR PRAKASHANCHAPTER - PROBABILITYEXERCISE - Solutions of NCERT Exemplar Problems (Fillers)5videos
PROBABILITY
- BOOK - KUMAR PRAKASHANCHAPTER - MATRICES EXERCISE - Practice Paper - 3 (Section - D)1videos
MATRICES
- BOOK - KUMAR PRAKASHANCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Practice Paper - 1 (Section - D)2videos
RELATIONS AND FUNCTIONS
Similar Questions
If P(A)=611,P(B)=511 amd P(A∪B)=711, find
(i) P(A∩B) (ii) P(A|B) (iii) P(B|A)00:58View SolutionA couple has two children,
(i) Find the probability that both children are males, if it is known that at least one of the children is male.
(ii) Find the probability that both children are females, if it is known that the elder child is a female.04:41View SolutionIf A and B are two events such that P(A∣B)=p,P(A)=p,P(B)=13 and P(A∪B)=59 then p = ……….
05:53View SolutionFor matrix A=⎡⎢⎣11112−32−13⎤⎥⎦ . Prove that , A3−6A2+5A+11I=0. Hence find A−1 using it .
05:18View SolutionLet : f:N→N be defined by f(n)={n+12 if n is oddn2 if n is even for all n∈N .
State whether the function f is bijective . Justify your answer.02:54View SolutionIf X be a random variable taking values x1,x2,x3,….,xn with probabilities P1,P2,P3,…..Pn, respectively. Then, Var (x) is equal to …….. .
06:03View SolutionThe probability distribution of the random variable X is given by
Then, the value of V(X) is equal to
 03:26View Solution
03:26View SolutionA random variable X takes values 0, 1, 2, 3,… with probability proportional to (x+1)(15)x.
P(X≥2) equals02:12View SolutionThe random variable takes the values 1,2,3,…….m. If P(X=n)=1m to each n, then the variance of X is
View SolutionThe probability function of a random variable is defined as
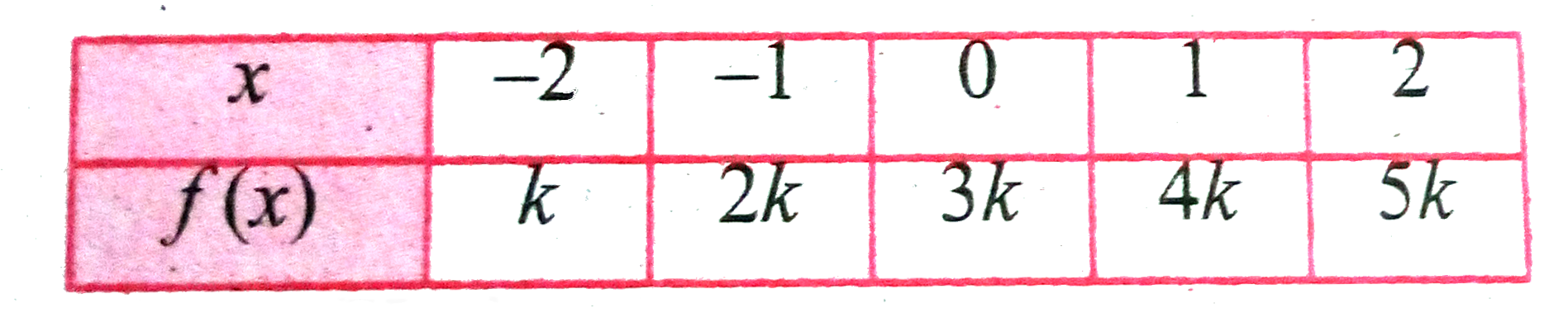
Then E(X) is equal toView SolutionIf the probability function of a random variable X is defined by P(X=k)=a(k+12k) for k=0,1,2,3,4,5, then the probability that X takes a prime value is
02:42View SolutionA discrete random variable X can take all possible integer values from 1 to K each with a probability 1K Its variance is
06:47View SolutionIf X be a random variable taking values x1,x2,x3,….,xn with probabilities P1,P2,P3,…..Pn, respectively. Then, Var (x) is equal to …….. .
05:13View SolutionA random variable X takes four values with probabilities 1+3x4,(1−x),1+2x4 and 1−4x4. Find the set of values of x for the variable X to have probability distribution.
05:56View SolutionRandom variable X takes the integral values from 1 to 100 having equal probability. Then find E(X), E(X2) and Var(X).
06:15View Solution

