PQ and PR are two infinite rays, QAR is an arc. Point lying in the shaded region excluding the boundary satisfies
|z−1|>2:|arg(z−1)|<π4
|z−1|>2:|arg(z−1)|<π2
|z+1|>2:|arg(z+1)|<π4
|z+1|>2:|arg(z+1)|<π2
The correct Answer is:C
Topper's Solved these Questions
- COMPLEX NUMBERS BOOK - ML KHANNACHAPTER - COMPLEX NUMBERS EXERCISE - Problem Set (3) Fill in the blanks
5 Videos
- COMPLEX NUMBERS BOOK - ML KHANNACHAPTER - COMPLEX NUMBERS EXERCISE - Problem Set (4) M.C.Q
26 Videos
- COMPLEX NUMBERS BOOK - ML KHANNACHAPTER - COMPLEX NUMBERS EXERCISE - Problem Set (3) (M.C.Q) Locus:
17 Videos
- CO-ORDINATE GEOMETRY OF THREE DIMENSIONBOOK - ML KHANNACHAPTER - CO-ORDINATE GEOMETRY OF THREE DIMENSIONEXERCISE - SELF ASSIGNMENT TEST
11 Videos
- CONCEPTS OF SET THEORY BOOK - ML KHANNACHAPTER - CONCEPTS OF SET THEORY EXERCISE - Self Assessment Test
13 Videos
Similar Questions
In the figure given below, PQRS is a square of side 14 cm and two semicircles are drawn inside of it with PQ and SR as diameters. Find the area of the shaded region in the figure.

View SolutionA corner point of a feasible region is a point in the reqion which is the of two boundary lines.
View Solution
Knowledge Check
P is any point inside or on the boundary of ΔABC having perimeter p and area Δ R is any point in the plane of ΔABC such that PR ≤ 5. the area of the region in which the point R lies is
A25π+5p+ΔB5π+25P+ΔC5π+5P+ΔD5(π+p)+25ΔABCD and EFGA are the squares of side 4 cm , each . In square ABCD, DMB and PMQ are the arcs of circles with centres at A and C respectively . In square AEFG , the shaded region is enclosed by two arcs of circles with centres at A and F , respectively . What is the ratio of the shaded regions of the squares ABCD and AEFG respectively .
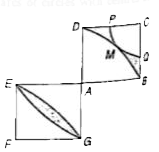 A2+π(√2−2)(π−2)B(π−2)2(√2+1−π)C43Dnone of these
A2+π(√2−2)(π−2)B(π−2)2(√2+1−π)C43Dnone of these
A corner point of a feasible region is a point in the reqion which is the of two boundary lines.
View SolutionPQRS is a diameter of a circle of radius 6 cm. The length PQ, QR and RS are equal Semicircle are drawn on PQ and QS as diameters. Find the area of the shaded region. Find also the length of boundaries of shaded portion.
View SolutionPQRS is a diameter of a circle of radius 6 cm. The length PQ, QR and RS are equal Semicircle are drawn on PQ and QS as diameters. Find the area of the shaded region. Find also the length of boundaries of shaded portion.
View SolutionShade the regions where points satisfy |x−y|<1.
View SolutionShade the regions where points satisfy |x−y|<1.
View SolutionAssertion Two infinitely long wires A and B carry unequal currents both in inward direction.

Then, there is only point (excluding the ponts at infinity), where net magnetic field is zero.
Reason That point lies between points A and B.
View Solution
