PQRS is a parallelogram. M and N are the mid-points of sides PQ and RS respectively. If XY is any line intersecting PS, MN and QR at X, O and Y respectively such that XY||PQ, then find the ratio in which O divides the line XY.
1:3
1:1
1:4
2:1
The correct Answer is:B
Step by step video, text & image solution for PQRS is a parallelogram. M and N are the mid-points of sides PQ and RS respectively. If XY is any line intersecting PS, MN and QR at X, O and Y respectively such that XY||PQ, then find the ratio in which O divides the line XY. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- IMO QUESTION PAPER 2018 SET B BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018 SET B EXERCISE - Everyday mathematics
10 Videos
- IMO QUESTION PAPER 2018 SET B BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018 SET B EXERCISE - Achievers Section
5 Videos
- IMO QUESTION PAPER 2018 SET ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018 SET AEXERCISE - ACHIEVERS SECTION
5 Videos
- IMO QUESTION PAPER 2020 SET 1BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020 SET 1EXERCISE - Achievers Section
5 Videos
Similar Questions
ABCD is a parallelogram. E and F are mid-point of side AB and CD respectively. AF and CE intersect diagonal BD at P & Q respectively. If BD = 15 cm, find PQ.

View Solution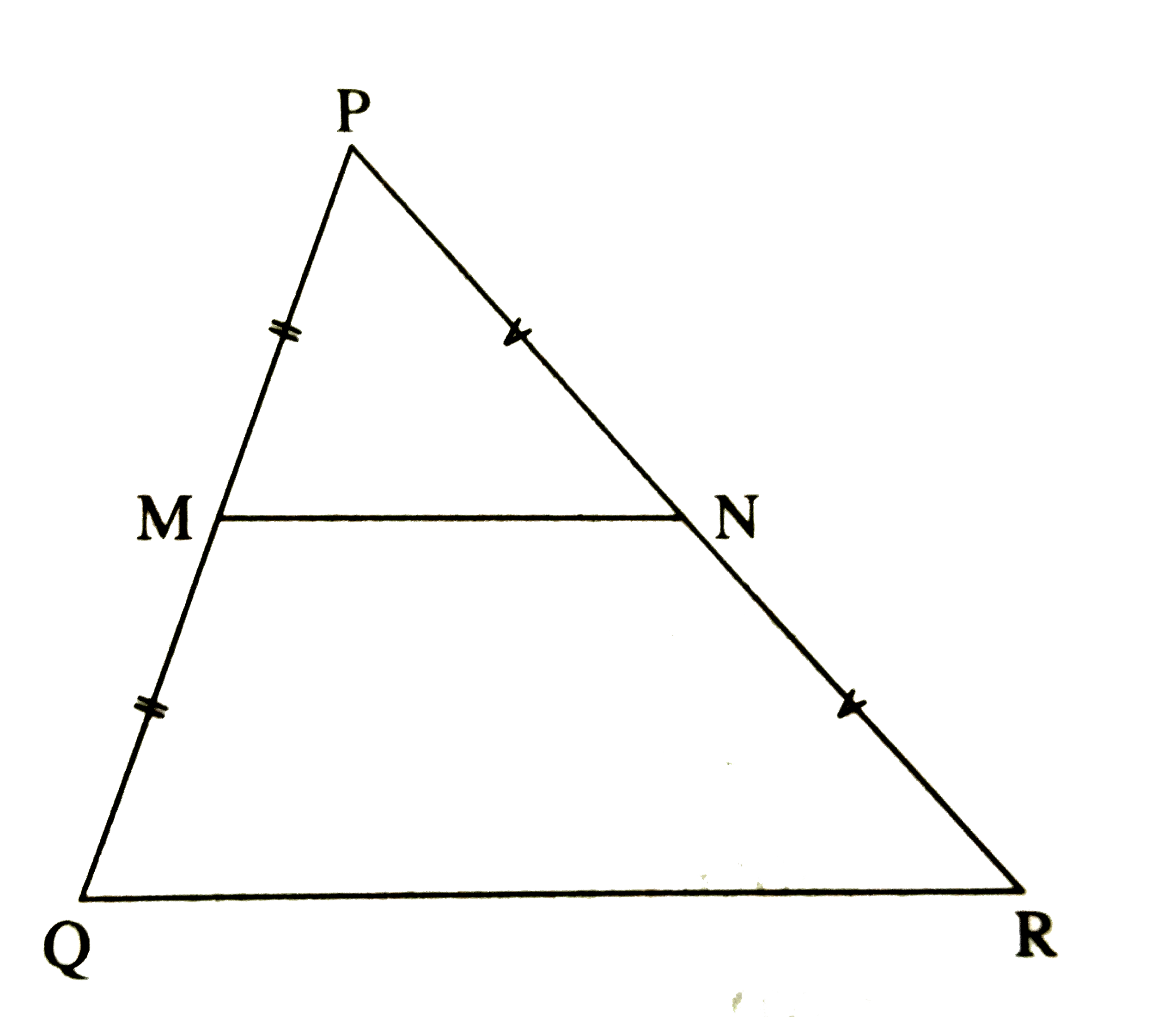
In the figure, M and N are the midpoints of sides PQ and PR respectively . If MN =6 cm then find QR. State your reason .
View Solution
Knowledge Check
Let □PQRS be a quadrilateral. If M and N are the mid-points of the sides PQ and RS respectively, then PS+QR=
A3¯¯¯¯¯¯¯¯MNB4¯¯¯¯¯¯¯¯MNC2¯¯¯¯¯¯¯¯MND2¯¯¯¯¯¯¯¯NMIn a square PQRS, X and Y are mid points of sides PS and QR respectively. XY and QS intersect a t O. Find the area of ΔXOS, if PQ = 8 cm.
A6 cm2B12 cm2C4 cm2D8 cm2OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3
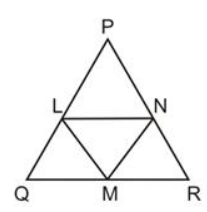
In A PQR, if PQ=PQ and L, M and N are the mid-points of the sides PQ, PR and RP respectively. Prove that LN=MN
View SolutionPQR is a triangle right-angled at Q. If X and Y are the mid-points of the sides PQ and QR respectively, then which one of the following is not correct?
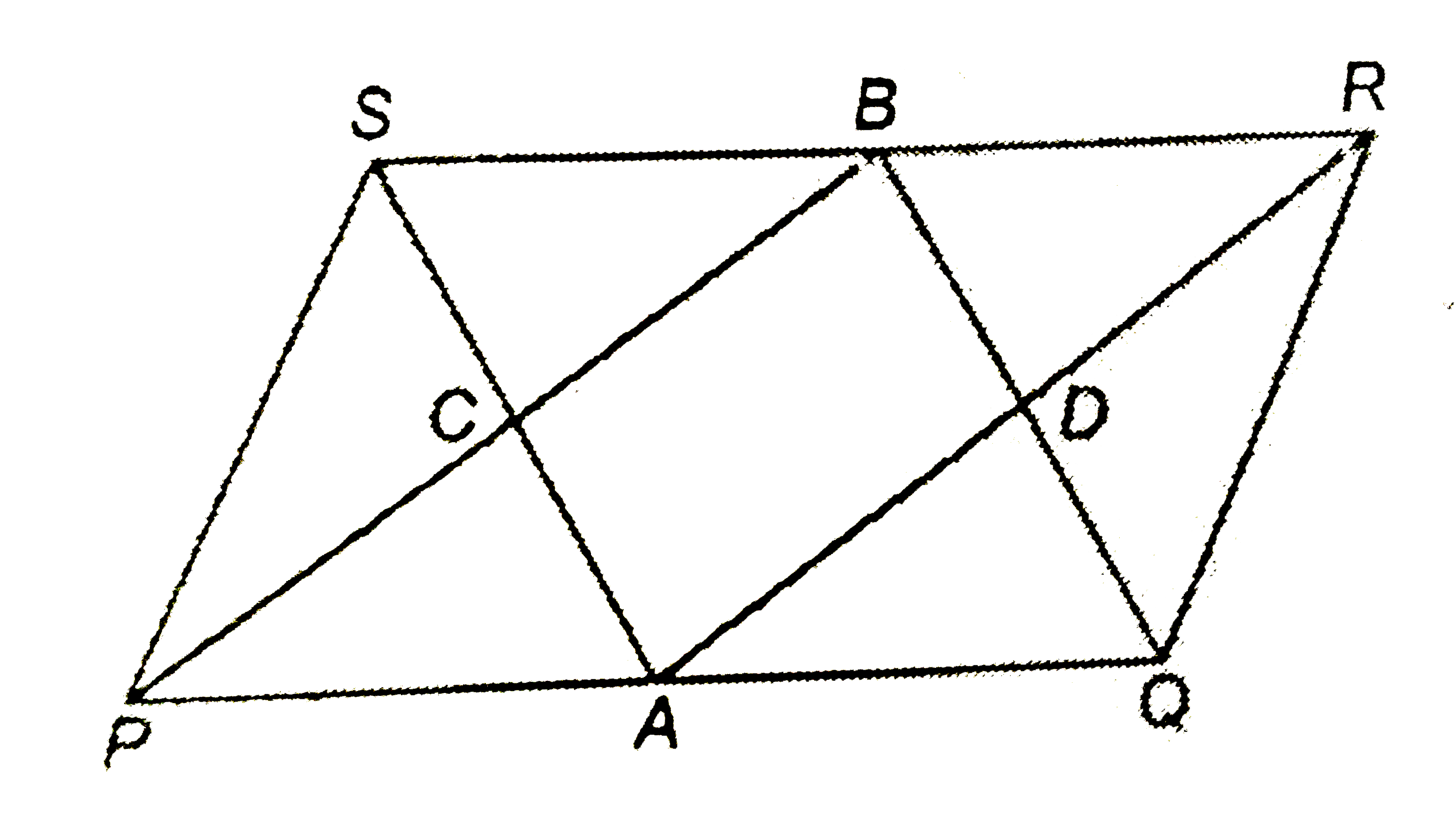
View SolutionIn the adjoining figure, PQRS is a parallelogram. A and B are the mid-points of PQ of SR respectively. If PS= BR, then prove that quadrilateral ADBC is a reactangle.
View SolutionΔPQR is right angled at Q. If x & y are the mid-points of sides PQ & QR respectively. Then which one is not true of the following:
View SolutionOPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
View Solution
