ΔPQR is right angled at Q. If x & y are the mid-points of sides PQ & QR respectively. Then which one is not true of the following:
RX2+PY2=5XY2
RX2+PY2=XY2+PR2
4(RX2+PY2)=5PR2
RX2+PY2=3[PQ2+QR2]
To solve the problem, we will analyze the properties of triangle PQR, which is right-angled at Q, and identify which statement among the given options is not true.
1. Draw Triangle PQR:
- Start by sketching triangle PQR with a right angle at Q. Label the vertices P, Q, and R.
2. Identify Midpoints:
- Mark point X as the midpoint of side PQ. This means that PX = XQ.
- Mark point Y as the midpoint of side QR. This means that QY = YR.
3. Apply the Midpoint Theorem:
- According to the Midpoint Theorem, if you connect the midpoints of two sides of a triangle, the segment connecting them is parallel to the third side and half its length. Therefore, segment XY is parallel to PR and XY = 1/2 PR.
4. Use the Pythagorean Theorem:
- Since triangle PQR is right-angled at Q, we can apply the Pythagorean theorem:
PR2=PQ2+QR2
5. Analyze the Given Statements:
- We are given four statements about the triangle and its midpoints. We need to check the validity of each statement based on the properties derived from the triangle and the midpoints.
6. Check Each Statement:
- For each option, apply the properties of the triangle and the midpoints to determine if the statement holds true.
- After evaluating the statements, identify which one does not conform to the properties established.
7. Conclusion:
- After checking all options, we find that option D is incorrect based on the properties of triangle PQR and the midpoints X and Y.
- Start by sketching triangle PQR with a right angle at Q. Label the vertices P, Q, and R.
- Mark point X as the midpoint of side PQ. This means that PX = XQ.
- Mark point Y as the midpoint of side QR. This means that QY = YR.
- According to the Midpoint Theorem, if you connect the midpoints of two sides of a triangle, the segment connecting them is parallel to the third side and half its length. Therefore, segment XY is parallel to PR and XY = 1/2 PR.
- Since triangle PQR is right-angled at Q, we can apply the Pythagorean theorem:
PR2=PQ2+QR2
- We are given four statements about the triangle and its midpoints. We need to check the validity of each statement based on the properties derived from the triangle and the midpoints.
- For each option, apply the properties of the triangle and the midpoints to determine if the statement holds true.
- After evaluating the statements, identify which one does not conform to the properties established.
- After checking all options, we find that option D is incorrect based on the properties of triangle PQR and the midpoints X and Y.
Topper's Solved these Questions
Similar Questions
Knowledge Check
PQR is a triangle. S and T are the midpoints of the sides PQ and PR respectively. Which of the following is TRUE?
I. Triangle PST is similar to triangle PQR.
II. ST = 1/2(QR)
III. ST is parallel to QR. / ST, QRAOnly I and IIBOnly II and IIICOnly I and IIIDAll I, II and IIILet □PQRS be a quadrilateral. If M and N are the mid-points of the sides PQ and RS respectively, then PS+QR=
A3¯¯¯¯¯¯¯¯MNB4¯¯¯¯¯¯¯¯MNC2¯¯¯¯¯¯¯¯MND2¯¯¯¯¯¯¯¯NMPQRSis a rectangle. Points A, B, C and D are the mid points of sides PQ,QR,RSandPSrespectively. If area of ΔPQR is 48cm2, then what is the area (in cm) of ΔBCD?
A24B6C16D12
In ΔPQR right angled at Q , PQ = 3 cm and PR = 6 cm .
Determine side QR.
View SolutionP and Q are the mid-points of the sides AB and BC, respectively, of ΔABC, right angled at B. Then:
View SolutionIn a right triangle ABC right angled at C, P and Q are points on the sides CA and CB respectively, which divide these sides in the ratio 2:1. Then, which of the following statements is true?
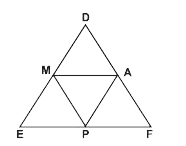
View SolutionM, A and P are the mid-points of the sides DE, DF and EF of Δ DEF respectively. Which of the following statements is true ?
View SolutionΔPQR is right angled at Q and measure of side PQ =14 cm., then what is the length (in cm.,)of side QR ?
View Solution